Zostrojíme matice Rx(α) , Ry(β), Rz(γ), zodpovedajúce rotáciám "okolo" jednotlivých osí o uhly α, β, γ - pozri vzorce (4), (5), (6) na tejto stránke mathworldu.
Trojrozmerná rotácia zobrazená na i-tom frame animácie zodpovedá ortogonálnej matici
Vi= Rx(α)i Ry(β)i Rz(γ)i.
Ak vhodne volíme počet framov a uhly α, β, γ, tak sa nám teleso "otočí zo všetkých strán" a rotácia telesa sa naviac pekne uzavrie, takže animáciu môžeme pustiť v slučke. Ja som na vygenerovanie nasledovného obrázku volil 48 framov a
α=π/8, β=π/12, γ=π/24.
Ako množinu zrotovaných bodov som zobral body na povrchu dvoch zakliesnených tórusov (Pozri predchádzajúci post). Upozorňujem, že výsledný animovaný gif má 2MB (mal by sa spustiť kliknutím na obrázok).
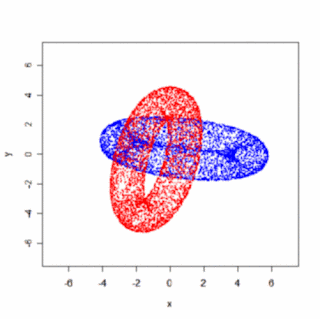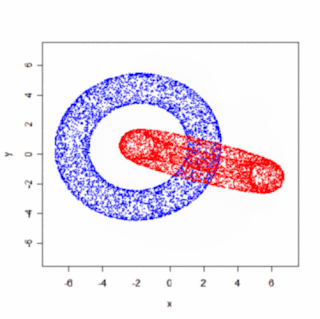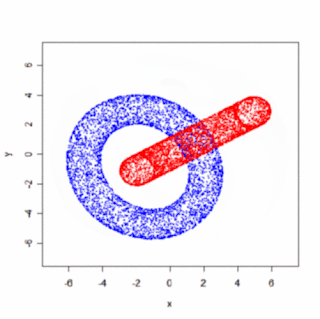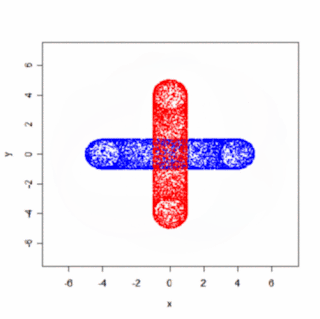 Samozrejme, oveľa efektnejšie by bolo použiť väčší počet framov (súčasne menšie uhly α, β, γ), "plné" telesá a prepočítavať viditeľnosť atď, ale princíp uzatvorenej slučky rotácií je jasný aj na takomto jednoduchom obrázku.
Samozrejme, oveľa efektnejšie by bolo použiť väčší počet framov (súčasne menšie uhly α, β, γ), "plné" telesá a prepočítavať viditeľnosť atď, ale princíp uzatvorenej slučky rotácií je jasný aj na takomto jednoduchom obrázku.Poznámka: Ak sa niekomu chce, mohol by skúsiť naprogramovať týmto spôsobom rotáciu tanečnice (alebo podobne zaujímavého objektu :). Očakávam, že ortogonálny (t.j. bez perspektívy) priemet akokoľvek komplikovanej rotácie by sa dal mentálne interpretovať dvomi spôsobmi, podobne ako v prípade slávnej tanečnice.
Žiadne komentáre:
Zverejnenie komentára