 V komentári k predchádzajúcemu príspevku navrhol Michal nasledovnú zaujímavú úlohu:
V komentári k predchádzajúcemu príspevku navrhol Michal nasledovnú zaujímavú úlohu:Koľko maximálne môžeme na nepriehľadnú guľu nakresliť bodiek tak, aby pre každú z týchto bodiek existoval smer pohľadu, z ktorého je vidieť len túto jednu bodku a žiadnu inú?
V zadaní predpokladáme, že z každého pohľadu vidíme celú polguľu aj s jej hranicou. Keďže pri takejto formulácii sa môžu vyskytnúť nejasnosti, uvediem aj nasledovné spresnenie.
Nájdite najväčšie prirodzené číslo n s vlastnosťou: Existuje 2n vektorov x1,...,xn,v1,...,vn v priestore Rm, m=3, spĺňajúcich
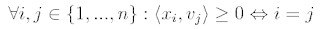
Alebo pomocou matíc:
Nájdite najväčšie prirodzené číslo n s vlastnosťou: Existujú matice X a V typu n×m, m=3, pre ktoré má matica XVT všetky diagonálne prvky nezáporné a všetky mimodiagonálne prvky záporné.
Tento problém je síce ľahko zrozumiteľný, ale nie celkom triviálny. A ak by sa ho niekomu podarilo matematicky precízne vyriešiť pre ľubovoľnerozmernú guľu, resp. z pohľadu druhej a tretej formulácie pre všetky dimenzie m, tak klobúk dolu.
Dodatok 1 (3.11.): Ako poznamenal v komentároch Peťo, ľahšia sa zdá byť verzia b), ktorá vznikne zámenou neostrej nerovnosti vo formulácii 2 na ostrú nerovnosť, resp. zámenou slov "nezáporné" a "záporné" na "kladné" a "nekladné". V tejto verzii je jasné, že optimálne n je minimálne 2m.
Dodatok 2 (3.11.): Tak som to pre m=3 (t.j. pre klasickú guľu) vyriešil počas prechádzky s Aďkou a Agátkou na Partizánskej lúke a ukázalo sa, že ten problém vôbec nie je až taký ťažký. Práve naopak; riešenie by mohol nájsť aj bystrý žiak základnej školy! Ostáva však záhadou, ako je možné, že ma to riešenie napadlo až po asi hodine premýšľania... :-)
18 komentárov:
a pozeram, ze si tiez fanusikom dobrej literatury (zoznam anglickych knih). s kamosmi tiez rozmyslame nad podobnym projektom, moj zoznam kniziek je sice kratsi, ale predsa.. tu: http://lehuta.blog.sme.sk/clanok.asp?cl=165113&bk=98362
Ak by sme tam mali ostru nerovnost miesto neostrej, vyzera to tak, ze by odpoved mohla byt n=2m.
Peter: Ak by sme tam mali ostrú nerovnosť (resp. polguľu bez hranice vo formulácii 1, alebo na diagonále kladné a mimo diagonály nezáporné čísla vo formulácii 3), tak je skutočne jasné, že maximálne n je väčšie rovné ako 2m; stačí zvoliť body xi ako plus minus jednotkové vektory a každé vi položiť rovné xi. OK
Ale poprvé, chcelo by to formálne dokázať, že n=2m je už maximum pre každé m (hoci sa do pre m=2,3 zdá byť geometricky jasné) a podruhé, čo je horšie, v zadaní je neostrá nerovnosť, čo sa síce zdá ako maličkosť, ale v skutočnosti to robí problém dosť odlišným. :-)
Ale zaujímavá úloha nie?
Hej, je to zaujimava uloha ;-)
Aj tvoja maticova formulacia je pekna.
Trosku to inak pripomina "kissing number problem", takze je mozne ze to nebude sranda.
Kedze sa mi zda ze neostra nerovnost to komplikuje, asi by som osobne zacal analyzou situacie s ostrou nerovnostou.
Pre n=2 vymysliet dokaz je pomerne lahke.
Pre n=3 a vyssie sa da ta dolna hranica n=2m dokazat lahko indukciou. Vyzera skoro uplne zrejme, pod tym myslim intuitivne jasne (mylim sa?), ze by n=2m malo byt zaroven optimalne (stale hovorim o ostrej nerovnosti). Nepokusal som sa to dokazat, ale ked budem mat trochu viac casu tak sa na to pozriem - ak to teda nebude uz tu na tvojom blogu medzicasom vyriesene ;-)
Michal, Peťo: Tak už som ten problém (všetky modifikácie) pre m=3 vyriešil a zaujímavé je na ňom predovšetkým to, že nás to primitívne riešenie ani jedného nenapadlo okamžite. :)
no, trivialne riesenia su casto najtazsie :-). ja si spominam na jeden poucny hlavolam z knihy F. Gahera, Logika pre kazdeho: dopln dalsie pismeno v rade (bodky su tam len kvoli zachovaniu grafickej podoby):
A.......E.F.
..B.C.D....G
vraj deti s tym nemaju problem... :-)
A: Môj tip je
A.......E.F..H.I...K.L.M.N...
..B.C.D....G.....J.........O.
:-)
Je to ono?
rado: je :-)
To s tými písmenami mi chvíľku trvalo (asi pol minúty), ale už mi to došlo. Pekné!
Rado: tak napíš to svoje triviálne riešenie. Mňa napadá iba trik s osemstenom, tak ako som dostal ten n=2m odhad.
riesenie ma napadlo pocas jazdy v MHD asi stvrt hodinu po prednaske... na tu gulu sa da umiestnit az kontinuum bodov, aby boli splnene podmienky zadania. ale musim uznat, velmi pekna uloha.
No a nie je to tak, že tých bodiek tam viem nahádzať ľubovoľne veľa? :)
Teda pre otvorené polgule stačí bodky nahádzať napr. na rovník, pre uzavreté na rovnobežku idúcu dostatočne tesne pod ním.
(Ale pár minút som sa aj ja najskôr poctivo snažil tie bodky rozmiestňovať nejako "rovnomerne" :D )
este aby som doplnil svoj predosly prispevok, tak to kontinuum je riesenie povodneho zadania, t.j. ak vidime aj body na okraji.
Avsak v modifikovanom zadani (t.j. kde okrajove body nevidime) tak sa uz neda umiestnit kontinuum bodov splnajucich podmienky.
Avsak existuje zasa sposob, ako sa da naukladat alef_0 bodov, aby boli splnene podmienky modifikovaneho zadania.
Teda v oboch tychto ulohach sa da naukladat na gulu az nekonecno bodov, avsak kym v povodnej ulohe to ide aj pre nespocitatelne nekonecno, tak v modifikovanej je to len spocitatelne nekonecno.
Pekné.
Ja som sa akosi automaticky zamyslel iba nad situáciou x_i = v_i, v ktorej sa veci majú inak.
Pekná úloha!
Tak ste to crackli! Fajn!
Tato uloha je pozoruhodna v tom, ze ako zadanie, tak aj riesenie sa da vysvetlit aj ziakovi zakladnej skoly, no pritom jej vyriesenie nemusi hned napadnut ani cloveka s doktoratom z matematiky.
Este otazka pre Slavomira: Je jasne, ze pre akekolvek konecne n je mozne naukladat n bodov na gulu, aby splnali to modifikovane zadanie s otvorenou hranicou polgule. Vedel by si vsak popisat ako je mozne naraz na tu gulu naukladat nekonecne (spocitatelne) vela bodov? To ma totiz takto narychlo nevie napadnut.
Slavomir: OK. Uz som si uvedomil ako je mozne naukladat naraz nekonecne vela bodov pre tu verziu ze hranicu polgule nevidime. Napriklad by to mohli byt body na "rovniku" so suradnicami (cos(pi/2^k),sin(pi/2^k),0) pre k=1,2,3,... Fajn.
Ano, podobne som tych alef_0 bodov umiestnil aj ja, napr.: (cos(1/k),sin(1/k),0), pre k=1,2,..
Ale moja uplne prvotna konstrukcia tej otvorenej ulohy bola tiez len pre lubovolny KONECNY pocet bodov a az medzi prvym a druhym prispevkom ma napadlo, ze sa to da umiestnit aj sucasne ako alef_0. A zaroven som si dokazal, ze viac ako alef_0 ich uz sucasne nemoze byt, takze preto som uz v tom druhom prispevku uviedol, ze najlepsie riesenie otvoreneho pripadu ma PRAVE alef_0 bodov.
Nemyslim vsak, ze je to az tak trivialna uloha pre zakladoskolaka, kedze jednak tam treba skonstruovat nekonecne vela bodov a tiez treba vediet rozlisovat medzi spocitatelnym a nespocitatelnym nekonecnom, co sa v ZS neuci :)
V zatvorenom pripade je to este v pohode, kedze staci zobrat napr. nejaku celu rovnobezku pod rovnikom (t.j. je to az 2^alef0 bodov), kedze je zrejme, ze pre kazdy taky bod existuje pohlad, v ktorom bude na okraji.
V otvorenom pripade vsak musi pre kazdy bod X existovat nejake d_X > 0, ze vsetky ostatne body su od neho vzdialene viac ako d_X (lebo ak by take kladne d_X neexistovalo, potom ak by sa bod X nemohol nachadzat SÁM v ziadnej ploche od ktorej okrajov ma kladnu vzdialenost, co vsak pozadujeme v otvorenom pripade). Takemuto bodu potom priradime kruh so stredom X a polomerom (d_X)/2. Zjavne kazdy takyto kruh ma kladny obsah a pre kazdu dvojicu bodov su aj taketo ich okolia disjunktne. A kedze su disjunktne, tak suma vsetkych ich obsahov nemoze presiahnut povrch gule, ktory je konecny (oznacme ho C).
Kazdemu prirodzenemu cislu n potom priradime mnozinu W_n takych bodov, ze ak S je obsah okolia takeho bodu (pozn.: okolim myslim kruh definovany vyssie), tak plati: (n-1) < (1/S) <= n (pozn.: zjavne kazdy bod potom pripadne do nejakej takej mnoziny W_i a zjednotenim vsetkych mnozin W_i dostaneme mnozinu vsetkych tych bodov).
Potom vsak suma vsetkych obsahov okoli bodov z mnoziny W_n je aspon |W_n|(1/n), a to ma byt nanajvys rovne povrchu gule, t.j. C, z coho dostamave, ze |W_n| <= C.n < nekonecno, teda W_n je konecna.
Nuz a zjednotenie spocitatelneho poctu konecnych mnozin je zjavne spocitatelna mnozina. Tym sme dokazali, ze vsetkych takych bodov moze byt najviac alef_0.
Staci teda uz len ukazat priklad, kde ich bude prave alef_0 a vyhrali sme. To tu vsak uz bolo uvedene, takze Q.E.D.
:)
Slavo: Pod tym vysvetlenim riesenia zakladoskolakovi som myslel vysvetlenie, ze sa da umiestnit lubovolny konecny pocet bodov. Samozrejme dobre viem (z mojich uz dlhorocnych pedagogickych skusenosti), ze rodiely v kardinalite nekonecnych mnozin nie su uplne jasne ani niektorym studentom vyssich rocnikov na matfyze. :-)
Zverejnenie komentára