28 decembra 2007
Otestujte si svoju geometrickú predstavivosť
1) Predstavte si teleso, ktorého všetky steny sú rovnako veľké pravidelné päťuholníky (dodecahedron). Koľko má toto teleso a) stien; b) hrán a c) vrcholov?
2) Predstavte si teleso, ktorého všetky steny sú rovnako veľké štvorce (kocka :-). Túto kocku rozpílime jedným rezom kolmým na niektorú hlavnú uhlopriečku (t.j. kolmo na spojnicu nejakej dvojice vrcholov neležiacich na spoločnej stene) na dve rovnaké telesá. Nech T je jedno z týchto dvoch telies. Koľko a) stien; b) hrán; c) vrcholov má teleso T?
3) Predstavte si teleso, ktorého všetky steny sú rovnako veľké rovnostranné trojuholníky (štvorsten :-). Stredy stien tohoto "veľkého" štvorstena V tvoria vrcholy "menšieho" štvorstena M. Koľkokrát má štvorsten M menšiu a) dĺžku hrán; b) obsah stien; c) objem, než štvorsten V?
Riešenia nájdete tu. Koľko z týchto deviatich úloh sa Vám podarilo správne vyriešiť? Akú metódu riešenia ste použili?
27 decembra 2007
Alex Vilenkin: Many Worlds in One
 Populárno-náučná kniha Alexa Vilenkina "Many Worlds in One" sa nezdržuje obohratými pesničkami z kozmológie a kvantovej mechaniky - len okrajovo sa v nej stretneme so štrbinami a strunami; relativistické dvojičky sa tu ani nemihnú. Tematickou náplňou Vilenkinovej knihy sú totiž úplne čerstvé myšlienky kozmológie, ktoré sú také fantastické, že by boli bizarné a depresívne aj pre veľkochovateľa Schördingerovych mačiek.
Populárno-náučná kniha Alexa Vilenkina "Many Worlds in One" sa nezdržuje obohratými pesničkami z kozmológie a kvantovej mechaniky - len okrajovo sa v nej stretneme so štrbinami a strunami; relativistické dvojičky sa tu ani nemihnú. Tematickou náplňou Vilenkinovej knihy sú totiž úplne čerstvé myšlienky kozmológie, ktoré sú také fantastické, že by boli bizarné a depresívne aj pre veľkochovateľa Schördingerovych mačiek.Viete si napríklad predstaviť fyzikálne a filozofické dôsledky predpokladu multiverza, pozostávajúceho z nekonečného počtu vesmírov, z ktorých každý má svoj náhodný počiatok v bezpríčinnej kvantovej fluktuácii vákua? A ako vlastne máme nájsť zmysel života v megavesmíre, v ktorom existuje nekonečne veľa identických kópií Zeme a čaká nás globálny výmaz akejkoľvek informácie o našej histórii?
"Many Worlds in One" je síce veľmi zaujímavá, no extrémne špekulatívna kniha vhodná pre čitateľa s triezvym pohľadom na dôsledky abstraktných matematických modelov aplikovaných ad extremum na náš konkrétny svet.
O knihe: Alex Vilenkin o svojej teórii (polhodinové audio). Rozsiahle review od Marka Troddena (profesor fyziky na Syracuse University). Ako vždy, kniha je u mňa k dispozícii na požičanie.
23 decembra 2007
Veselé Vianoce!

M (práve prišla z obchodu): Doniesla som Ti na zjedenie šišku.
A (s plačom): Nieeee, nechcem jesť sisku.
M: A prečo?
A: Siska pichá!
M: Ah. Ale takúto šišku.
A (zarazená): To nie je siska. To je buchta.
M: Daj si tú béžovú čiapku.
A: Ten macko (na čiapke) sa volá Béžo?
V byte nešla elektrina, tak som vyšiel na chodbu a skúsil som, či ide výťah, aby som zistil, či je výpadok v celom vchode.
A: Co robíš tata?
T: Skúšam, či ide elektrina.A: Elektrina príde výtahom?
M: No poď holka.
A (prekvapene): Ja nie som holka, ja som oblecená!
T: Aj ja by som chcel takú bundičku ako máš ty.A: Takú malú?T: Nie, takú mäkkú.
A: Takú mäkkú a veľkú?
T: Áno.A (s ľústostivým pohľadom): Ked bude mat Agátka korunky, tak kúpi tatovi mäkkú a velkú bundicku.
Štastné a veselé!
22 decembra 2007
Pytagorova pavučina
 Na obrázku vľavo sú čiernymi bodkami zaznačené všetky usporiadané dvojice (x,y) prirodzených čísel menších ako 4000, pre ktoré je odmocnina z x2+y2 celé číslo, čiže x a y sú celočíselné odvesny pravouhlých trojuholníkov s celočíselnou preponou. Vidíme, že tieto body nie sú rozmiestnené úplne chaoticky, ale majú určitú štruktúru.
Na obrázku vľavo sú čiernymi bodkami zaznačené všetky usporiadané dvojice (x,y) prirodzených čísel menších ako 4000, pre ktoré je odmocnina z x2+y2 celé číslo, čiže x a y sú celočíselné odvesny pravouhlých trojuholníkov s celočíselnou preponou. Vidíme, že tieto body nie sú rozmiestnené úplne chaoticky, ale majú určitú štruktúru.Vedeli by ste vysvetliť pôvod "priamok", t.j. množín bodov (x,y), pre ktoré y=αx? Aké sú hodnoty konštanty α pre priamky, ktoré sú na obrázku najvýraznejšie? Menej viditeľná, ale pri pozornom pohľade nespochybniteľná je aj štruktúra rôznych "oblúkov". Vedeli by ste vysvetliť aj pôvod týchto oblúkov?
Pod vysvetlením nejakej "vizuálnej štruktúry" rozumiem matematické tvrdenie, na základe ktorého by matematik mohol vznik tejto štruktúry predvídať aj bez nakreslenia obrázku.
Poznámka: Prvé dve otázky sú samozrejme jednoduché, avšak ako vysvetliť pôvod oblúkov ma počas tých pár minút, ktoré som venoval rozmýšľaniu nad týmto problémom, nenapadlo. Ale Vy budete možno bystrejší. Alebo niečo nájdete na webe pod hlavičkou "Pythagorean triples".
19 decembra 2007
Nebude matika! Pôjdeme do divadla ...
 Konečne. Všetko nasvedčuje tomu, že sa konečne našiel hrdina, ktorý sa nebojí otvorene povedať, že
Konečne. Všetko nasvedčuje tomu, že sa konečne našiel hrdina, ktorý sa nebojí otvorene povedať, že"matematika plne prispieva k znižovaniu IQ študentov a populácie Slovenska, vedie k vytváraniu bezmennej, plastickej masy, ktorá nepozná žiadne kultúrne hodnoty a žije ako limitovaná a ohlúpnutá skupina bez znalostí a záujmu o reálne potreby človeka." (Prečítajte si tento blogový príspevok.)
Reálnou potrebou človeka je totiž vedieť obsluhovať zákazníkov zahraničných reštaurácií v piatich svetových jazykoch a spisovne sa pozhovárať o futbale a o Hviezdoslavovi pri práci za pásom výrobnej linky. Za týmto účelom naozaj neexistuje lepšia voľba, než je novou školskou reformou v posledných dvoch ročníkoch gymnázií stanoviť ako jediné povinné predmety dva cudzie jazyky, slovenčinu a samozrejme telesnú výchovu.
A teraz vážne.
Jazyky sú síce veľmi dôležitý nástroj na komunikovanie myšlienok, ale na to, aby nám boli užitočné, musíme byť schopní v prvom rade produkovať tie myšlienky (možno s výnimkou divadelníctva). Nemá zmysel vedieť spisovne a plynule rozprávať v cudzom jazyku - a ani v slovenčine - bez toho, aby sme mali o čom rozprávať. Dovolím si tvrdiť, že väčšina ľudí, ktorí pracujú duševne a pritom tvorivo (okrem umelcov) využíva, alebo by s výhodou mohla využívať v nejakej forme matematiku, prípadne štatistiku (ktorá je ale tiež v podstate matematikou) - od statikov, strojníkov, farmaceutov, ekonómov, programátorov až po meteorológov a psychológov.
Aby sme sa rozumeli; samozrejme nie som a priori proti reforme osnov matematiky a v zásade ani proti tomu, aby sa matematiku nemuseli učiť žiaci, ktorí na to jednoducho nemajú. Ale ak má byť matematika pre študentov posledných dvoch ročníkov gymnázií nepovinná, tak s podmienkou, že naozaj každý bude mať zo zákona možnosť si ju zvoliť - a to v primeranom rozsahu.
17 decembra 2007
Trojuholníky a determinant
 Intuícia mi hovorí, že by mala platiť nasledovná veta; pokúsme sa ju dokázať (prípadne vyvrátiť kontrapríkladom, ale to by ma trochu mrzelo :)
Intuícia mi hovorí, že by mala platiť nasledovná veta; pokúsme sa ju dokázať (prípadne vyvrátiť kontrapríkladom, ale to by ma trochu mrzelo :)Nech trojuholník abc je podmnožinou trojuholníka ABC. Vyjadrime body a,b,c ako konvexné kombinácie bodov A,B,C, t.j. nech

kde αi1+αi2+αi3=1 pre všetky i a αij je nezáporné pre všetky i,j. Uvažujme maticu

Potom obsah Sabc trojuholníka abc a obsah SABC trojuholníka ABC sú vo vzťahu:

Poznámky: Myslím si, že táto úloha má potenciál inšpirovať veľa ďalších otázok. Napríklad: Platí analogické tvrdenie nielen pre trojuholníky, ale aj pre simplexy vyšších dimenzií (t.j. napríklad pre štvorsten)? Platilo by toto tvrdenie aj ak by trojuholník abc nebol podmnožinou trojuholníka ABC (a αij by mohli byť aj záporné)? Aký geometrický vzťah medzi trojuholníkmi (simplexami) reprezentujú špeciálne typy matíc M? Alebo: Ak by sme definovali determinant matice pomocou pomeru plôch trojuholníkov, nedali by sa priamo "vidieť" niektoré inak nie celkom prehľadné tvrdenia o determinante? Napríklad nebolo by možné geometricky zdôvodniť tvrdenie, že súčin determinantov matíc je determinant súčinu týchto matíc? A tak ďalej.
Poznámka 18.12.: Práve som zistil, že toto tvrdenie je známe; pozri vzťah (4) na tejto stránke mathworldu :-( ;-). Každopádne, poznámky pod znením úlohy môžu snáď viesť aj k niečomu aspoň trochu novému ...
Poznámka 23.12.: Všimnime si, že z našeho tvrdenia okamžite vyplýva to, že ak plocha trojuholníka ABC je jedna, tak koeficienty α11, α12 a α13 zodpovedajú presne plochám trojuholníkov aBC, AaC a ABa :-)
07 decembra 2007
Pascalov hrad
 Keď som si dnes s dcérkou staval hrad, napadla ma nasledovná úloha :-)
Keď som si dnes s dcérkou staval hrad, napadla ma nasledovná úloha :-)Majme pyramídu, ktorá pozostáva z 1+2+3+...+k ohybných mostíkov tvaru približne zodpovedajúcemu symbolu Π, ako je znázornené na priloženom obrázku pre k=3. Predpokladajme, že "nožičky" mostíkov sú presne zvislé a všetky majú rovnakú dĺžku δ. Najnižšie položené mostíky stoja na podložke (vo všeobecnosti nerovnej) a vyššie položené mostíky majú nožičky presne na strede "striešok" patriacim dvom nižšie položeným mostíkom. Takže tvar celej ohybnej konštrukcie závisí od y-ových súradníc bodov B1,...,Bk, Bk+1, ktorými sa konštrukcia dotýka podložky. Symbolom A označme bod ležiaci na strede striešky najvyššie položeného mostíka.
a) Nájdite vzorec, ktorý udáva závislosť y-ovej súradnice bodu A od δ a od y-ových súradníc bodov B1,...,Bk, Bk+1.
b) Dá sa čakať, že čím väčšie je k, tým "vodorovnejšia" je strieška najvyššie položeného mostíka? (Chcel som mať čo najrovnejšiu základňu na čo najvyšší komín ;-)
Poznámka 8.12.: Časť a) je jednoduchá, taká stredoškolská, ale podľa mňa celkom zábavná. Časť b) je už trochu komplikovanejšia a zámerne som ju neformuloval úplne striktne. Aplikácia matematiky sa totiž veľmi často začína práve takýmito neformálnymi otázkami v "ľudskej reči" a prvou úlohou je práve nájsť zmysluplnú transformáciu daného problému do reči rigoróznej matematiky.
06 decembra 2007
ARRA 2007
 Krátko po zverejnení nelichotivého vysvedčenia slovenského stredného školstva v podobe správy PISA 2006, máme tu vysvedčenie pre naše vysoké školstvo a vedu od agentúry ARRA. Ani tentokrát sa nebudem púšťať do dlhých hodnotiacich úvah (hoci mi nedá nepripomenúť, že naša fakulta dopadla ako obvykle výborne; teda aspoň na slovenské pomery). Zameriam sa len na jeden možno trochu neopatrne formulovaný výrok uverejnený v článku SME pochádzajúci od nášho bývalého rektora profesora Ferdinanda Devínskeho:
Krátko po zverejnení nelichotivého vysvedčenia slovenského stredného školstva v podobe správy PISA 2006, máme tu vysvedčenie pre naše vysoké školstvo a vedu od agentúry ARRA. Ani tentokrát sa nebudem púšťať do dlhých hodnotiacich úvah (hoci mi nedá nepripomenúť, že naša fakulta dopadla ako obvykle výborne; teda aspoň na slovenské pomery). Zameriam sa len na jeden možno trochu neopatrne formulovaný výrok uverejnený v článku SME pochádzajúci od nášho bývalého rektora profesora Ferdinanda Devínskeho:"Ak odrátame akadémiu, tak špičkových vedcov máme na vysokých školách 35 z 1 500 profesorov. To je 2,3 percenta. Toľko ľudí je nejakým spôsobom schopných konkurovať vede vo svete alebo Európe. To je desivé číslo."
Kde sa zobralo číslo 35? Čo to znamená "konkurovať vede vo svete alebo Európe"? A kto sú vlastne tí naši super vedci? Z hodnotiacej správy sa dozvieme odpoveď len na prvú z týchto otázok a aj to iba čiastočnú. Kľúčovým ukazovateľom je pritom takzvaný Hirschov index publikačnej činnosti.
Globálny prínos práce vedca je príliš široký a vágny pojem na to, aby ho bolo možné dokonale kvantifikovať jedným číslom; často sa preto vedú vzrušené debaty o používaní toho či onoho kritéria. V tomto smere je Hirschov index (h-index) populárnou novinkou a jeho cieľom je zohľadniť ako kvantitu, tak aj kvalitu publikačnej činnosti. Hirschov index vedca V vypočítame ako maximálne n, pre ktoré platí: V má aspoň n publikácií, z ktorých každá má aspoň n citácií. (Podotýkam, že ARRA, celkom správne, neberie do úvahy samocitácie.) Výhody a nevýhody h-indexu sa podľa mňa celkom vyvážene popisujú na stránkach wikipedie.
Takže ako rozhodovala ARRA o tom, kto je špičkový vedec? Podľa ARRA je špičkový vedec ten, kto má nadlimitný Hirschov index, pričom limitný index je rôzny pre rôzne vedné odbory. Extrémnymi prípadmi sú na jednej strane matematika, kde je limitný h-index 6 a na druhej strane biológia, ktorá má limitný h-index 18. Hodnotiaca správa však neudáva akým spôsobom k týmto limitným indexom prišla, len informuje, že jedným z kritérií je priemerný počet citácii jednej práce v danom vednom odbore. (Napríklad matematika ako taká má priemerný počet citácií na jednu prácu 2,77, zatiaľčo biológia ich má až 15,67, teda jednoduchý zaokrúhlený konštantný násobok to nebude.) Súhlasil by som s takouto definíciou "špičkového vedca", avšak je pre mňa veľkou záhadou, prečo musí mať napríklad biológ h-index aspoň 18, aby bol "nejakým spôsobom schopný konkurovať vede vo svete alebo Európe". Aké sú dôvody myslieť si, že biológ s h-indexom povedzme 10 medzinárodnej konkurencie nie je schopný? Aký je vlastne h-index pre "priemerného" biológa vo svete a v Európe?
Samozrejme, nijako nenapádam aktivitu ARRA vyselektovať najlepších vedcov; naopak, veľmi to vítam a to aj napriek tomu, že akákoľvek kvantifikácia vedeckej práce bude niekoho nespravodlivo znevýhodňovať a iného nie celkom zaslúžene zvýhodňovať (napríklad toho, koho primárnou motiváciou je dosiahnutie vysokej hodnoty špecifického kvantitatívneho ukazovateľa). Nakoniec, medzi špičkovými slovenskými vedcami je 12 matematikov, z ktorých viacerých určite osobne poznám, a ktorých prácu si veľmi vážim.
Skrátka zoznam tých najlepších slovenských vedcov by som naozaj veľmi uvítal - mohol by byť jedným z podnetov pre zlepšenie situácie v našej vede. Ale na druhej strane je namieste byť trochu opatrnejší vo formuláciách, ktoré marginalizujú medzinárodný význam publikačnej aktivity všetkých ostatných. Naviac, bolo by vhodné upozorňovať na to, aké mimoriadne ťažké je vyšvihnúť sa medzi svetovú špičku v našich skromných podmienkach.
Poznámka 7.12.: Predpokladám, že limitné indexy boli v ARRA stanovené nejakou premyslenou (hoci nezverejnenou) metódou, ale ak by som mal ja zvoliť limitný h-index pre "špičkového slovenského matematika", tak by som ho založil na nejakej dobre definovanej skupine vedcov, napríklad všetkých matematikov z nejakej univerzity svetového významu. Za limitný h-index by som zobral medián h-indexov v tejto skupine ľudí (priemer by asi nebol najvhodnejší). Takýmto postupom by bol špičkový slovenský matematik skrátka ten, ktorý by patril k lepšej polovici aj na danej "svetovej" univerzite. Presne takto isto by som volil limitné indexy pre ostatné vedecké odbory, čím by vznikla do istej miery naozaj spravodlivá báza na medziodborové porovnávanie. (Inou možnosťou je zaradiť medzi špičkového slovenského vedca takého, ktorý je povedzme medzi prvými 5000 vedcami podľa h-indexu vedcov z celého sveta v danej oblasti.)
Poznámka 8.12. A: Dnes sa na SME objavil informatívnejší a opatrnejšie formulovaný článok o špičkových profesoroch, v ktorom sa už napríklad spomína, že "máme veľa aktívnych a výnimočných docentov" :-) Základný problém, t.j. ako dospeli v ARRA k limitným h-indexom, sa však ani v tomto článku neobjasňuje. Akú výpovednú hodnotu má mať údaj (napríklad "35 z 1500") založený na nezdôvodnených parametroch, ktoré sa v princípe dajú nastaviť tak, aby sme dosiahli akýkoľvek vopred požadovaný výsledok?
A ešte jedna poznámka: ARRA zabudla zverejniť na akom mieste v Európe a na svete je slovenská veda v počte publikácií v špičkových časopisoch v pomere k financiám, ktoré sa u nás vynakladajú na vedu. V tomto ukazovateli by Slovensko bezpochyby bolo v absolútnej svetovej špičke ;-)
Poznámka 8.12. B: ARRA už dávnejšie zverejnila menný zoznam najlepších slovenských chemikov (h-index aspoň 15) a fyzikov (h-index aspoň 13). V súvislosti s ním je veľmi zaujímavý zoznam približne 500 najlepších svetových chemikov zoradených podľa h-indexu. Každý z nich má h-index aspoň 50 ...
05 decembra 2007
PISA 2006
 Včera prebehla správami zaujímavá informácia o výsledkoch testu PISA 2006, ktorého cieľom bolo zmerať školské vedomosti a schopnosti 15 ročných mládežníkov z krajín OECD (pozri napr. článok SME). Nebudem tu analyzovať príčiny neúspechu Slovenska a úspechu Fínska; tie chápu takmer všetci (pozri napríklad článok z Izraela), bohužiaľ okrem tých ľudí, ktorí majú/mali reálnu moc naše školstvo postaviť na nohy.
Včera prebehla správami zaujímavá informácia o výsledkoch testu PISA 2006, ktorého cieľom bolo zmerať školské vedomosti a schopnosti 15 ročných mládežníkov z krajín OECD (pozri napr. článok SME). Nebudem tu analyzovať príčiny neúspechu Slovenska a úspechu Fínska; tie chápu takmer všetci (pozri napríklad článok z Izraela), bohužiaľ okrem tých ľudí, ktorí majú/mali reálnu moc naše školstvo postaviť na nohy.Upozorniť by som však chcel na stránku projektu PISA 2006, na ktorej je možné získať sumárne štatistiky o odpovediach na jednotlivé otázky vo všetkých zúčastnených krajinách. Zaujíma Vás napríklad, či v teste z matematiky dopadli na Slovensku lepšie chlapci alebo dievčatá? A čo by ste povedali: V čítaní dopadli lepšie tí, ktorí majú doma umývačku riadu, alebo tí, ktorí umývačku nemajú? Na uvedenej stránke sa dajú získať tieto a mnoho iných zábavných aj poučných štatistík.
24 novembra 2007
Mat tretím ťahom: dva v jednom
Táto moja "kompozícia" je len taký náhodný úkaz, ale inak na Slovensku máme veľmi silnú skupinu serióznych kompozičných šachistov. Jeden z nich je bývalý matfyzák a môj dlhoročný priateľ Juraj Lörinc.
Poznámka 30.11.: Ako zistil ruziklan vo svojej databáze šachových úloh (pozri komentáre), obidva tieto problémy boli publikované už v roku 1900 (Galickij). Takže žiadna originálna kompozícia to nie je :-)
22 novembra 2007
Multivesmír, determinizmus a náhodnosť
 Hneď na začiatku by som chcel upozorniť, že nie som fyzik, takže všetky moje nasledujúce špekulácie sú len čosi ako science fiction a treba ich brať s rezervou. S veľkou rezervou.
Hneď na začiatku by som chcel upozorniť, že nie som fyzik, takže všetky moje nasledujúce špekulácie sú len čosi ako science fiction a treba ich brať s rezervou. S veľkou rezervou.21 novembra 2007
Odmocniny ortogonálnych matíc
Nech k je prirodzené číslo a nech U je ortogonálna matica typu m krát m. Nájdite predpis pre počet a metódu konštrukcie všetkých ortogonálnych matíc V, pre ktoré platí U=Vk.
Keď som sa nad týmto problémom trochu zamyslel, dospel som k názoru, že práve takáto úloha môže byť vhodná na "kolektívne" riešenie. Urobme teda pedagogický experiment: Keď Vás napadne niečo nové a relevantné, napíšte to do komentáru a spoločne sa budeme snažiť prísť problému na kĺb. Ja sám sa nebudem snažiť tento problém intenzívne riešiť, iba možno občas napíšem nejaký motivačný postreh. Tiež sa nebudem pýtať na riešenie mojich kolegov, ktorí sa veľmi dobre v danej problematike orientujú, pretože vážne hrozí, že by nám úlohu hneď vyriešili a pokazili by nám radosť z objavovania :-) Možno sa nám podarí trochu poodhaliť kreatívny proces matematického uvažovania a pritom sa aj vzdeláme vo veľmi zaujímavej a dôležitej oblasti. Takže na úvod len niekoľko postrehov.
Postreh 1 (algebraický): Ak je k párne, tak je nutnou podmienkou existencie aspoň jednej k-tej odmocniny matice U rovnosť det(U)=1, t.j. U musí byť takzvanou špeciálnou ortogonálnou maticou, resp. maticou rotácie. Dôkaz: Všimnime si, že determinant akejkoľvek ortogonálnej matice V môže byť iba +1 alebo -1: Z definície ortogonality V máme VVT=I, kde I je jednotková matica a zo základných vlastností determinantu máme
Postreh 2 (geometrický): Ak by sme hľadali riešenia V s determinantom 1, tak vlastne hľadáme takú "rotáciu" V, ktorej k-násobným opakovaným použitím dostaneme zadanú "rotáciu" U. Dá sa ale tušiť, že každá rotácia U sa dá poskladať z k-opakovaných rotácií V, t.j. naša domnienka je, že det(U)=1 je postačujúcou podmienkou na existenciu aspoň jednej k-tej odmocniny matice U.
Postreh 3 (algebraický): Pre niektoré ortogonálne matice U existuje viac ako jedna k-ta odmocnina: Napríklad, ako jednotková matica I, tak aj matica -I je ortogonálna a platí I=I.I, ale aj I=(-I)(-I).
Postreh 4 (4.12.07): Už pre jednotkovú maticu I typu 2x2 existuje nespočítateľne veľa druhých odmocnín! Ako sa dá ľahko skontrolovať, pre každé reálne θ je nasledovná matica ortogonálna druhá odmocnina matice I.

Postreh 5 (5.12.07). Predchádzajúca matica je len špeciálny prípad širokej triedy ortogonálnych druhých odmocnín jednotkovej matice I typu mxm. Môžete si skontrolovať, že ortogonálnou druhou odmocninou matice I je každá matica V tvaru

kde u1,...,um je systém navzájom kolmých vektorov dĺžky 1 a i1,...,im sú 0 alebo 1. To teda znamená, že jednotková matica mxm pre akékoľvek m>=2 má nekonečne veľa ortogonálnych druhých odmocnín.
A ako som na tento predpis pre V prišiel? Ako je to so zdanlivo komplikovanými matematickými vzorcami časté, myšlienky, ktoré k nim vedú, sú založené na veľmi jednoduchých geometrických predstavách, analógiách a mechanických formálnych postupoch. (Niekedy je však ťažké tieto postupy zrozumiteľne popísať. Na druhej strane občas akoby niektorí prehnane ctižiadostiví matematici svoje postupy zámerne tajili aby sa mohli vyťahovať svojimi úžasnými formulkami. Podobne ako David Copperfield neprezradí sériu triviálnych fínt, na ktorých sa zakladá na prvé videnie prekvapivý výsledný efekt :-)
Takže najprv som si uvedomil, že matica z Postrehu 4 zodpovedá preklopeniu roviny okolo nejakej priamky prechádzajúcej počiatkom súradnicovej sústavy. To je ale taká transformácia roviny, ktorá nechá jednotkový smerový vektor u danej priamky nezmenený a druhý jednotkový vektor, kolmý na u, preklopí na opačný. Analogické transformácie sa predsa dajú skonštruovať v ľubovoľnom priestore! Ak by sme mali akýkoľvek systém navzájom kolmých jednotkových vektorov, tak môžeme vytvoriť transformáciu, ktorá niektoré z týchto vektorov preklopí a iné nechá nezmenené. Je úplne zrejmé, že dvojnásobné použitie tejto transformácie opäť vráti všetky vektory do pôvodnej polohy! Je už len záležitosťou základnej techniky lineárnej algebry z prvého ročníka formálne zapísať maticu V, ktorá tomuto preklápaniu zodpovedá.
Čo sa teda týka ortogonálnych druhých odmocnín jednotkových matíc, tento špeciálny prípad pôvodného problému už máme skoro vyriešený, hoci ešte by sme sa mohli spýtať, či existujú aj ortogonálne druhé odmocniny jednotkovej matice, ktoré nie sú typu matice V popísanej vyššie. (Tipol by som si, že nie.) Trochu ťažšie, ale stále nie úplne všeobecné otázky sú nasledovné: Ako skonštruovať triedu všetkých k-tych odmocnín jednotkovej matice pre k>2? Je množina všetkých tretích ortogonálnych odmocnín jednotkovej matice typu 2x2 konečná, alebo je nekonečná? Ako skonštruovať druhú odmocninu z akejkoľvek zadanej ortogonálnej matice (s determinantom 1)?
...
Máte nejaké nápady?
Rotácia telies
Zostrojíme matice Rx(α) , Ry(β), Rz(γ), zodpovedajúce rotáciám "okolo" jednotlivých osí o uhly α, β, γ - pozri vzorce (4), (5), (6) na tejto stránke mathworldu.
Trojrozmerná rotácia zobrazená na i-tom frame animácie zodpovedá ortogonálnej matici
Ak vhodne volíme počet framov a uhly α, β, γ, tak sa nám teleso "otočí zo všetkých strán" a rotácia telesa sa naviac pekne uzavrie, takže animáciu môžeme pustiť v slučke. Ja som na vygenerovanie nasledovného obrázku volil 48 framov a
Ako množinu zrotovaných bodov som zobral body na povrchu dvoch zakliesnených tórusov (Pozri predchádzajúci post). Upozorňujem, že výsledný animovaný gif má 2MB (mal by sa spustiť kliknutím na obrázok).
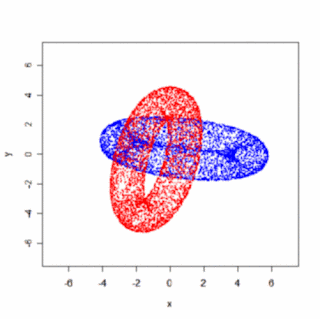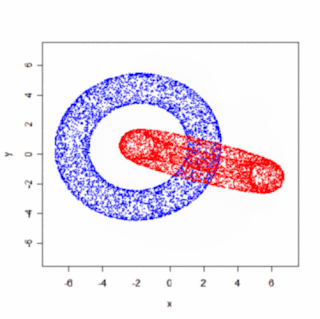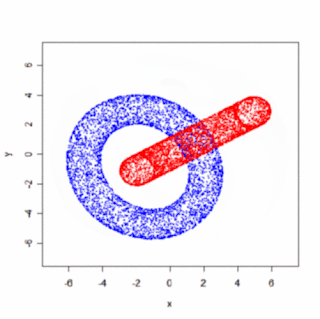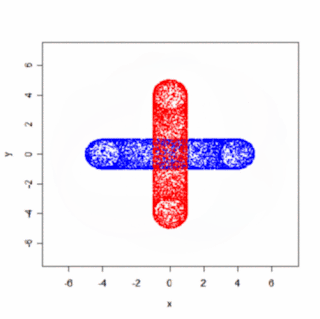 Samozrejme, oveľa efektnejšie by bolo použiť väčší počet framov (súčasne menšie uhly α, β, γ), "plné" telesá a prepočítavať viditeľnosť atď, ale princíp uzatvorenej slučky rotácií je jasný aj na takomto jednoduchom obrázku.
Samozrejme, oveľa efektnejšie by bolo použiť väčší počet framov (súčasne menšie uhly α, β, γ), "plné" telesá a prepočítavať viditeľnosť atď, ale princíp uzatvorenej slučky rotácií je jasný aj na takomto jednoduchom obrázku.Poznámka: Ak sa niekomu chce, mohol by skúsiť naprogramovať týmto spôsobom rotáciu tanečnice (alebo podobne zaujímavého objektu :). Očakávam, že ortogonálny (t.j. bez perspektívy) priemet akokoľvek komplikovanej rotácie by sa dal mentálne interpretovať dvomi spôsobmi, podobne ako v prípade slávnej tanečnice.
15 novembra 2007
Náhodné body na tóruse

Ak chcete vedieť detaily, pozrite si môj program v jazyku R.
12 novembra 2007
Zacyklený milionár
 V dvoch tučných nepriehľadných obálkach sú peniaze, pričom viem, že v jednej z týchto obálok je dvojnásobok sumy v druhej obálke. Dostal som možnosť vybrať si ľubovoľnú z týchto dvoch obálok a peniaze z nej si ponechať. Avšak akonáhle jednu obálku otvorím, už sa nemôžem rozhodnúť pre tú druhú.
V dvoch tučných nepriehľadných obálkach sú peniaze, pričom viem, že v jednej z týchto obálok je dvojnásobok sumy v druhej obálke. Dostal som možnosť vybrať si ľubovoľnú z týchto dvoch obálok a peniaze z nej si ponechať. Avšak akonáhle jednu obálku otvorím, už sa nemôžem rozhodnúť pre tú druhú.Náhodne som si zvolil jednu obálku, no tesne pred otvorením ma napadla výborná myšlienka. Moja obálka obsahuje sumu X a ja s istotou viem, že tá druhá obálka obsahuje sumu X/2, alebo sumu 2X. To znamená, že ak si vyberiem tú druhú obálku, môžem v porovnaní s momentálnym stavom stratiť X/2, ale získať môžem až X. Zjavne je výhodné zobrať si tú druhú obálku! Potešil som sa svojej bystrej úvahe a obálky som si vymenil. Už som sa chystal preveriť si svoj zisk, no v tom ma napadla ďalšia výborná myšlienka. Moja obálka obsahuje sumu X ...
Obálky si vymieňam dodnes. Občas mi síce v hlave vŕta iracionálny červík pochybnosti, ale moje logické úvahy sú predsa nepriestrelné. Alebo nie?
Poznámka: Tento problém patrí k matematickému folklóru (pozri link v komentároch); moja vlastná je len jeho formulácia :-)
Delenie zlatého prútu II
 Predpokladajme rovnakú situáciu ako v predošlom príspevku, avšak s nasledovnými možnosťami výberu Vášho úlomku: a) Dostanete najmenší z úlomkov; b) Dostanete polovicu z druhého najväčšieho úlomku. Ktoré pravidlo by ste si vybrali?
Predpokladajme rovnakú situáciu ako v predošlom príspevku, avšak s nasledovnými možnosťami výberu Vášho úlomku: a) Dostanete najmenší z úlomkov; b) Dostanete polovicu z druhého najväčšieho úlomku. Ktoré pravidlo by ste si vybrali?Poznámka: Predpokladáme, že deliace body vyberáme nezávisle a rovnomerne náhodne na celom prúte. Inak tento príklad je ťažší (a odpoveď je menej jednoznačná) ako v predchádzajúcom príspevku; dôvody však nebudem zatiaľ rozoberať.
Poznámka 13.11.: V komentároch už máme správne riešenie založené na simuláciách; zaujímavé by však bolo aj presné (analytické) riešenie. Podujme sa na to niekto?
09 novembra 2007
Delenie zlatého prútu I
 Zlatý prút bude rozdelený na tri úlomky dvomi náhodnými rezmi, pričom jeden z týchto úlomkov máte dostať Vy. Môžete si vopred zvoliť jedno z nasledovných pravidiel výberu Vášho úlomku: a) Dostanete "prostredný" úlomok, t.j. ten, ktorý neobsahuje ani jeden z okrajov pôvodného prútu; b) Dostanete ten úlomok, na ktorom leží stred pôvodného prútu. Ktoré z týchto dvoch pravidiel je pre Vás výhodnejšie? Alebo sú obe pravidlá "ekvivalentné"?
Zlatý prút bude rozdelený na tri úlomky dvomi náhodnými rezmi, pričom jeden z týchto úlomkov máte dostať Vy. Môžete si vopred zvoliť jedno z nasledovných pravidiel výberu Vášho úlomku: a) Dostanete "prostredný" úlomok, t.j. ten, ktorý neobsahuje ani jeden z okrajov pôvodného prútu; b) Dostanete ten úlomok, na ktorom leží stred pôvodného prútu. Ktoré z týchto dvoch pravidiel je pre Vás výhodnejšie? Alebo sú obe pravidlá "ekvivalentné"?Netranzitívne kocky
 Pre dve kocky K a L s očíslovanými stenami označme symbolom P[K>L] pravdepodobnosť, že pri súčasnom hode týmito kockami padne na kocke K väčšie číslo ako na kocke L. Nájdite očíslovanie strán troch kociek A,B,C tak, aby súčasne platilo:
Pre dve kocky K a L s očíslovanými stenami označme symbolom P[K>L] pravdepodobnosť, že pri súčasnom hode týmito kockami padne na kocke K väčšie číslo ako na kocke L. Nájdite očíslovanie strán troch kociek A,B,C tak, aby súčasne platilo:P[A>B]>1/2, P[B>C]>1/2, P[C>A]>1/2.
Poznámka: Tento príklad partí k pravdepodobnostnému "folklóru". Zaujímavejšou a ťažšou úlohou je nájsť očíslovania štyroch kociek A,B,C,D, pre ktoré platí P[A>B]>1/2, P[B>C]>1/2, P[C>D]>1/2 a P[D>A]>1/2.
07 novembra 2007
Pravdepodobnosť a demokracia
My však poďme trochu ďalej a položme si otázku: "Aká by bola situácia, ak by bol sudca A lepší než sudca B, napríklad ak by sme mali pA=90%, pB=89,9% a pC=50%"? Dá sa ľahko ukázať, že potom by optimálnou rozhodovacou stratégiou poroty ako celku bolo rozhodovať len na základe sudcu A, t.j. úplne ignorovať hlas nielen mincového sudcu C, ale aj relatívne veľmi dobrého sudcu B. Ako je to teda vo všeobecnosti s výberom optimálnej skupinovej stratégie rozhodovania troch sudcov v závislosti od ich pravdepodobností správneho rozhodnutia pA, pB a pC?
Všetkých stratégií skupinového rozhodovania trojčlennej poroty je, v istom dobre definovanom zmysle, 256 a pre každú kombináciu pravdepodobností pA, pB, pC je možné nájsť tú najlepšiu stratégiu metódou "hrubej sily" na počítači. Keď položíme pevne pA=0,75 a pre rôzne kombinácie hodnôt pB a pC v rozmedzí 0,5 až 1 farebne zaznačíme optimálnu stratégiu, dostaneme nasledovný obrázok.

Farby oranžová, červená a žltá zodpovedajú situáciám, kedy je optimálne ignorovať všetkých okrem toho, kto správne rozhoduje s najväčšou pravdepodobnosťou. (Predstavte si napríklad rodiča s dvomi malými deťmi :-) Modrou farbou je zobrazená oblasť tých dvojíc (pB,pC), pri ktorých je optimálnym „demokratický“, t.j. väčšinový rozhodovací systém. Vidíme, že tento systém je optimálny, voľne povedané, v prípade, že sú všetci traja podobne, ale zďaleka nie nutne rovnako dobrí. Všimnite si napríklad, že bod so súradnicami (0,72; 0,69) leží v modrej oblasti, takže pre pA=0,75, pB=0,72 a pC=0,69 je optimálnym väčšinový rozhodovací systém.
Na nasledovnom obrázku sú znázornené pravdepodobnosti správnych rozhodnutí poroty pri optimálnej stratégii skupinového rozhodovania (opäť v závislosti od pB a pC pri pevnom pA=0,75).
 Z obrázku a aj bez neho je zrejmé, že žiadna stratégia plne založená na rozhodovaní len jediného človeka nemôže priniesť kvalitu rozhodovania lepšiu ako je kvalita samotného "diktátora". To sa ale nedá povedať o demokratickej rozhodovacej stratégii. V súlade s intuíciou aj našim modelom, demokratická stratégia vedie k takému rozhodovaniu celej skupiny, ktoré môže byť podstatne kvalitnejšie, než umožňujú schopnosti ktoréhokoľvek zúčastneného jednotlivca.
Z obrázku a aj bez neho je zrejmé, že žiadna stratégia plne založená na rozhodovaní len jediného človeka nemôže priniesť kvalitu rozhodovania lepšiu ako je kvalita samotného "diktátora". To sa ale nedá povedať o demokratickej rozhodovacej stratégii. V súlade s intuíciou aj našim modelom, demokratická stratégia vedie k takému rozhodovaniu celej skupiny, ktoré môže byť podstatne kvalitnejšie, než umožňujú schopnosti ktoréhokoľvek zúčastneného jednotlivca.Poznámky: Pochopiteľne na hraniciach medzi oblasťami prislúchajúcimi rôznym optimálnym stratégiám je súčasne optimálnych viacero stratégií. Najzaujímavejší je tento fenomén asi v bodoch, kde sa stretávajú dve "diktátorské" optimálne stratégie s demokratickou optimálnou stratégiou (zelené bodíky). Inak teoreticky zaujímavé, ale asi pomerne ťažké, by bolo študovať optimálne stratégie pre počet sudcov väčší ako 3. Počet všetkých stratégií pre n sudcov je 2 na (2 na n), čiže už pre povedzme n=7 neprichádza výpočet hrubou silou do úvahy.
Poznámka 8.11.: Kuriózne optimálne stratégie skupinového rozhodovania vznikajú vtedy, keď niektorí zo sudcov majú pravdepodobnosť správneho rozhodnutia menšiu ako 50%. Napríklad ak pA=80%, pB=15% a pC=50%, potom je najlepšou stratégiou rozhodovania ignorovať sudcov A, C a ako výsledok zobrať opačné rozhodnutie ako je rozhodnutie sudcu B :-)
31 októbra 2007
Monte Carlo a mnohorozmerné simplexy



30 októbra 2007
Monte Carlo a mnohorozmerné kocky
Poznámka 31.10.: Na obrázkoch je pochopiteľne len dvojrozmerný priemet daných hyperkociek; konkrétne ortogonálny priemet na náhodne zvolenú rovinu.



25 októbra 2007
Konštantná šírka
 V poslednej dobe mám menej času na zábavu s blogom, takže opäť len jednoduchá úloha :-)
V poslednej dobe mám menej času na zábavu s blogom, takže opäť len jednoduchá úloha :-)Šírkou (ohraničeného) rovinného útvaru v smere vektora v nazvime minimálnu šírku nekonečne dlhého pásu, ktorý daný útvar obsahuje a je rovnobežný s vektorom v. Napríklad pre kosoštvorec na obrázku je s1 šírka v smere v1 a s2 je šírka v smere v2. (Menej formálna definícia je šírka tieňa daného telesa osvetlovaného z nekonečne vzdialeného zdroja v smere vektora v.) Je zrejmé, že kruh má konštantnú šírku vo všetkých možných smeroch. Otázka znie: Existuje ešte nejaký iný konvexný rovinný útvar, ktorý má šírku rovnakú vo všetkých smeroch?
23 októbra 2007
Lúč
 Zo štyroch zrkadiel sme zostavili štvorcovú komoru a z rohu (0,0) sme v smere bodu (x,1) vyslali lúč (pozri obrázok). Koľkokrát sa tento lúč odrazí od stien komory kým nenarazí presne do niektorého z rohov?
Zo štyroch zrkadiel sme zostavili štvorcovú komoru a z rohu (0,0) sme v smere bodu (x,1) vyslali lúč (pozri obrázok). Koľkokrát sa tento lúč odrazí od stien komory kým nenarazí presne do niektorého z rohov?Poznámka: Uvažujeme idealizovaný prípad, t.j. matematicky presný štvorec, nekonečne tenký lúč a dokonalé odrazy. Napríklad ak x=0,2, tak je počet odrazov 4, ak je x=0,75 tak je počet odrazov 5 a podobne. Úlohou je popísať čo najjednoduchší postup (vzorec, algoritmus), ktorým sa dá z x dospieť k počtu odrazov. Svoje riešenia tejto úlohy (aj iných úloh) môžete napísať do komentárov.
Poznámka 27.10.: Úlohu nám už vyriešila gurama (pozri komentáre).
19 októbra 2007
Sťahovanie vo Flatlande
 Vo Flatlande je potrebné premiestniť objekt cez chodbu na obrázku. Nájdite objekt s čo najväčšou plochou, ktorý je touto chodbou možné premiestniť.
Vo Flatlande je potrebné premiestniť objekt cez chodbu na obrázku. Nájdite objekt s čo najväčšou plochou, ktorý je touto chodbou možné premiestniť.Poznámky: Objekt možno ľubovoľne posúvať, ťahať a rotovať, ale samozrejme nie deformovať. Napríklad je takto možné premiestniť červený trojuholník na obrázku s plochou 1 meter štvorcový. Je však možné presunúť aj objekt s väčšou plochou? Dodám ešte, že túto úlohu mám z jednej knihy (zatiaľ neprezradím z ktorej) a podľa formulácie riešenia v tejto knihe sa zdá, že dosiaľ nie je dokázané, že to ich riešenie je naozaj optimálne.
17 októbra 2007
Rotujúca tanečnica
Čierny tieň na obrázku sa samozrejme netočí ani v smere, ani proti smeru hodinových ručičiek; je to len dvojrozmerný objekt. Finta je v tom, že presne takýto tieň by tanečnica vrhala nech by sa točila v ktoromkoľvek z týchto dvoch smerov. Náš mozog pritom z tieňa automaticky rekonštruuje trojrozmerný objekt a ten sa môže točiť len v jedinom smere; skrátka si musí vybrať jednu z dvoch navzájom sa vylučujúcich alternatív (podobne je to v prípade Neckerovej kocky).
Pre ktorú možnosť sa teda náš mozog rozhodne? To nechajme pre nejaký psychologický blog, ale povedal by som, že tu môže hrať rolu "priming". V pôvodnom článku spomínané vysvetlenie na základe dominancie niektorej z hemisfér sa mi zdá byť nepravdepodobné. Totiž podľa toho vysvetlenia by som mal byť viac umelecky ako matematicky založený (tanečnica sa mi pri prvom pohľade točila v smere hodinových ručičiek). A to by som si už asi bol býval všimol.
Čo je však práve na tejto tanečnici také výnimočné? Moja odpoveď znie: Skoro nič. Ak by sme totiž rotovali akékoľvek teleso v smere hodinových ručičiek, tak jeho tieň bude presne taký istý, ako keby sme rotovali proti smeru hodinových ručičiek zrkadlovo preklopenú verziu toho istého telesa. (Všimnite si, že tanečnica má zodvihnutú ľavú nohu pri rotácii proti smeru hodinových ručičiek a pravú nohu ak ju vidíme rotovať v smere hodinových ručičiek.) Ľahko si to uvedomíme v dvoch rozmeroch napríklad pomocou tohoto obrázku:

A prečo som napísal že na tanečnici nie je skoro nič výnimočné? Pretože si myslím, že rotovať teleso-tanečnicu je obzvlášť účinné na dosiahnutie daného efektu. Sme totiž veľmi dobre prispôsobení práve na vytváranie si trojrozmernej predstavy ľudí; postavy nie sú pre nás len "nejaké" telesá, ale veľmi dôležité telesá a mozog s nimi zrejme narába trochu inak ako s inými objektmi. Je to možno niečo ako známy fakt, že tváre rozpoznávame oveľa spoľahlivejšie než iné, podobne komplexné obrazce.
Poznámka 18.10.: Tipol by som si, že ak by sme ako rotujúci objekt použili postavu, ktorá zdraví zdvihnutou rukou, tak väčšina z nás by mala tendenciu vidieť rotáciu v takom smere, aby náš trojrozmerný mentálny model mal zdvihnutú pravú ruku.
Acknowledgements: Na rotujúcu tanečnicu ma upozornil kolega Ján Somorčík.
16 októbra 2007
Vymyslené hádzanie

Skúste si to. Buď si náhádžte výsledky mincou, alebo si napíšte na papier postupnosť 120 vymyslených výsledkov H/Z (hlava/znak) a snažte sa, aby Vaša postupnosť pôsobila čo najnáhodnejšie.
Poznámka. Existuje veľké množstvo podobných testov na "pravosť" generovania náhodných hodnôt. Napríklad: Rozdeľte svoju postupnosť 120 výsledkov na 30 úsekov po štyri výsledky a spočítajte, koľko z týchto štvoríc je typu HHHH, ZZZZ, HZZZ, ZHHH, HHZZ, ZZHH, HHHZ alebo ZZZH. Ak je takýchto štvoríc 10 alebo menej, zrejme ste si danú postupnosť vymysleli. Ak by ste totiž naozaj hádzali mincou, bola by pravdepodobnosť takéhoto výsledku približne len 0,05. To čo sme tu urobili sa v štatistickej terminológii nazýva test hypotézy o pravdepodobnosti p binomického rozdelenia na hladine významnosti 5 percent.
15 októbra 2007
Pokrývanie šachovnice
 Máme "šachovnicu" so 78 poliami zobrazenú na obrázku. Je ju možné úplne pokryť
Máme "šachovnicu" so 78 poliami zobrazenú na obrázku. Je ju možné úplne pokryťa) 39 dvojpolíčkovými obdĺžnikmi ?
b) 26 trojpolíčkovými obdĺžnikmi ?
c) 26 trojpolíčkovými L-kami ?
Poznámka 7.11.: časti a) aj b) už máme vyriešené (pozri komentáre). Pre úlohu c) ešte nemáme v komentároch riešenie, ale aspoň ja som už konečne riešenie našiel :-) keď povoľujeme
12 októbra 2007
Green dwarf alien

Kniha Michaela Drosnina "The Bible code" je podľa mňa jeden z vrcholných  počinov v oblasti získavania slávy a zarábania na ľudskej senzáciechtivosti a nevzdelanosti. Podobne ako som to urobil ja, môžete si aj Vy vziať prakticky akýkoľvek text (nemusí to byť ani hebrejská biblia ako v Drosninovej knihe) a pomocou počítača v ňom nájdete desiatky podobných tajných odkazov a proroctiev. Pri experimentovaní s mojim programíkom som zistil, že zadané štvorpísmenové slovo sa v matici 50x75 písmen bežného textu dá nájsť takmer isto, päťpísmenové často a šesťpísmenové občas. (Samozrejme, závisí to na písmenách zadaného slova; slová obsahujúce Q sa obvykle nenájdu, ani keď sú krátke.) Inak celé je to možné pekne a pomerne jednoducho podložiť matematicky: aj keby sme generovali základný text úplne náhodne, tak by pravdepodobnosť výskytu zadaného ekvidištančného reťazca písmen bola pomerne vysoká. Možno si niekedy nájdem čas a stručne to pre Vás spíšem.
počinov v oblasti získavania slávy a zarábania na ľudskej senzáciechtivosti a nevzdelanosti. Podobne ako som to urobil ja, môžete si aj Vy vziať prakticky akýkoľvek text (nemusí to byť ani hebrejská biblia ako v Drosninovej knihe) a pomocou počítača v ňom nájdete desiatky podobných tajných odkazov a proroctiev. Pri experimentovaní s mojim programíkom som zistil, že zadané štvorpísmenové slovo sa v matici 50x75 písmen bežného textu dá nájsť takmer isto, päťpísmenové často a šesťpísmenové občas. (Samozrejme, závisí to na písmenách zadaného slova; slová obsahujúce Q sa obvykle nenájdu, ani keď sú krátke.) Inak celé je to možné pekne a pomerne jednoducho podložiť matematicky: aj keby sme generovali základný text úplne náhodne, tak by pravdepodobnosť výskytu zadaného ekvidištančného reťazca písmen bola pomerne vysoká. Možno si niekedy nájdem čas a stručne to pre Vás spíšem.
09 októbra 2007
Blink a šachové algoritmy
 Moja dnešná malá špekulácia, inšpirovaná knihou Blink, sa týka tajomstva našej schopnosti rýchleho intuitívneho ohodnotenia objektu či situácie a toho, prečo je často takéto hodnotenie presné, ale v niektorých prípadoch sa nechá oklamať jednoduchými trikmi.
Moja dnešná malá špekulácia, inšpirovaná knihou Blink, sa týka tajomstva našej schopnosti rýchleho intuitívneho ohodnotenia objektu či situácie a toho, prečo je často takéto hodnotenie presné, ale v niektorých prípadoch sa nechá oklamať jednoduchými trikmi. Základom väčšiny šachových programov sú dva úplne odlišné "funkčné moduly". Prvý z nich je modul na vytváranie stromu popisujúceho možné vetvenie hry podľa potenciálnych ťahov. Bez tohoto modulu by program väčšinou nenašiel ani tie najjednoduchšie kombinácie. Druhý z týchto modulov slúži na heuristické ohodnocovanie pozícií a zahŕňa množstvo rôznorodých strategických faktorov odvodených z dlhodobých hráčskych skúseností. Takéto hodnotenie je pritom možné robiť mnohými spôsobmi; jeden z nich je napríklad použiť trénované umelé neurónové siete, ktoré reprezentujú informáciu len implicitne.
Základom väčšiny šachových programov sú dva úplne odlišné "funkčné moduly". Prvý z nich je modul na vytváranie stromu popisujúceho možné vetvenie hry podľa potenciálnych ťahov. Bez tohoto modulu by program väčšinou nenašiel ani tie najjednoduchšie kombinácie. Druhý z týchto modulov slúži na heuristické ohodnocovanie pozícií a zahŕňa množstvo rôznorodých strategických faktorov odvodených z dlhodobých hráčskych skúseností. Takéto hodnotenie je pritom možné robiť mnohými spôsobmi; jeden z nich je napríklad použiť trénované umelé neurónové siete, ktoré reprezentujú informáciu len implicitne.Naše myslenie pozostávajúce z nadväznosti vedomých krokov je možné prirovnať k postupnému vytváraniu stromu pozícií. Na druhej strane našim inštinktom a našej intuícii - automatickému, rýchlemu a ťažko zdôvodniteľnému mysleniu bez izolovateľných medzikrokov je analogické heuristické ohodnocovanie koncových pozícií umelou neurónovou sieťou. Tieto moduly našej mysli veľmi úzko spolupracujú, podobne ako je to v šachovom programe: Bez sekvenčného uvažovania by sme síce mohli existovať, ale nášmu správaniu by chýbala plánovitosť a naopak, bez inštinktov a intuície by sme len slepo brázdili priestor všetkých možností a nevedeli by sme sa nijako rozhodnúť; chýbal by nám smer a uspokojivý cieľ.
Poznámka 9.10.: Táto predstava až prekvapivo dobre zodpovedá skutočne pozorovaným prípadom patologického uvažovania z knihy A. Damasia Decartes' error; akoby moje dva metaforické moduly skutočne existovali a bolo by ich možné "vyradiť z činnosti".
Poznámka 11.10.: Práve sa v online vydaní SME v sekcii Veda objavil článok o knihe Blink v českom preklade (Okamih).
Poznámka 14.10.: Vypočujte si podcast knihy Blink (mp3).
08 októbra 2007
Bláznivé percentá
 Nedarí sa mi dokázať nasledovné tvrdenie.
Nedarí sa mi dokázať nasledovné tvrdenie.Pomôžete mi ? :-)
V krabici sú červené loptičky, modré loptičky, červené kocky a modré kocky, pričom loptičiek a kociek je rovnaký počet. Z krabice si zoberieme 98 percent červených kociek, ale iba 88 percent červených loptičiek. Taktiež si zoberieme 80 percent modrých kociek, ale iba 76 percent modrých loptičiek. Potom istotne budeme mať viac kociek ako loptičiek.
Upozornenie: Riešenie nájdete v komentároch.
03 októbra 2007
Náhodné permutácie
 Náhodné permutácie sú mojou obľúbenou témou na ilustráciu základných techník v teórii pravdepodobnosti. Keď som na Wolfram demonstrations objavil programík na grafické znázorňovanie cyklov náhodnej permutácie, rozhodol som sa, že o náhodných permutáciách napíšem krátky príspevok do blogu. Možno táto téma niekoho zaujme; bola by napríklad vhodná na bakalársku (a možno aj diplomovú) prácu pre teoretickejšie orientovaného matematika.
Náhodné permutácie sú mojou obľúbenou témou na ilustráciu základných techník v teórii pravdepodobnosti. Keď som na Wolfram demonstrations objavil programík na grafické znázorňovanie cyklov náhodnej permutácie, rozhodol som sa, že o náhodných permutáciách napíšem krátky príspevok do blogu. Možno táto téma niekoho zaujme; bola by napríklad vhodná na bakalársku (a možno aj diplomovú) prácu pre teoretickejšie orientovaného matematika.Uvažujme postupnosť (1,2,...,n), ktorú "dokonale" náhodne premiešame, napríklad pomocou jednoduchého Fisherovho-Yatsovho algoritmu. Tým dosiahneme to, že každá z n! možných výsledných permutácií má pravdepodobnosť 1/n!. Uvedomme si, že každá permutácia rozloží množinu čísiel 1,...,n na niekoľko podmnožín zodpovedajúcich "cyklom" (pozri ilustračný obrázok vľavo hore pre n=24).
Napríklad pre n=6 má permutácia (2,1,4,6,5,3) tri cykly: cyklus „...-3-4-6-3-4-6-...“ dĺžky 3 (pretože pôvodná pozícia 3 je v novej permutácii obsadená číslom 4, pôvodná pozícia 4 je obsadená číslom 6 a pôvodná pozícia 6 je obsadená číslom 3), ďalej cyklus „...-1-2-1-2-1-...“ dĺžky 2, a cyklus „...-5-5-5-...“ dĺžky 1. Permutácia na ilustračnom obrázku má 5 cyklov dĺžok 1,1,3,5 a 14.
Z pravdepodobnostného hľadiska je práve zaujímavé študovať charakteristiky počtu cyklov a ich dĺžok v náhodnej permutácií.
Najklasickejší problém z oblasti náhodných permutácií, ktorý sa objavuje na prednáškach z pravdepodobnosti po celom svete, môžeme formulovať napríklad takto: Sekretárka náhodne rozdelí n (rôznych) listov do n (rôznych) obálok s adresami. Aká je pravdepodobnosť, že aspoň jeden list vloží do správnej obálky? V reči náhodných permutácií a cyklov sa pýtame na otázku aká je pravdepodobnosť, že náhodná permutácia n čísiel bude mať aspoň jeden cyklus dĺžky jedna. To je možné vyriešiť jednoduchou aplikáciou princípu zapojenia vypojenia. Na tomto príklade je tiež zaujímavé to, že pre n ide do nekonečna sa výsledná pravdepodobnosť blíži presne k 1-1/e.
Veľa podobných otázok je vyriešených v podrobnom článku Wikipédie pomocou techniky vytvárajúcich funkcií. Niektoré z týchto otázok sa však dajú vyriešiť oveľa elementárnejšie, priamočiarym využitím linearity strednej hodnoty. Takto je napríklad možné ukázať, že stredná hodnota počtu cyklov dĺžky k je presne 1/k (nezávisle na n). To znamená, že v priemere sa vygeneruje jeden cyklus dĺžky 1, "pol" cyklu dĺžky dva, atď. Z toho tiež okamžite plynie, že stredná hodnota počtu všetkých cyklov je n-té harmonické číslo H(n) . To je aj pre veľké n kontraintuitívne nízke číslo; napríklad stredný počet cyklov náhodnej permutácie milión čísiel je približne 14,4. Dá sa preto tušiť, že v náhodnej permutácií by sa mali s "veľkou pravdepodobnosťou" vyskytovať "veľké cykly". Skutočne to tak je; napríklad jednoduchým trikom je možné ukázať, že pravdepodobnosť výskytu cyklu obsahujúceho nadpolovičnú väčšinu čísiel je H(n)-H(n/2). (Pre jednoduchosť berieme n párne.) Hodnota H(n)-H(n/2) konverguje k číslu ln(2), čo je približne 0,693. To znamená, že pre veľké n vznikne s pravdepodobnosťou zhruba 70% v náhodnej permutácii n čísiel cyklus obsahujúci nadpolovičnú väčšinu čísiel.
02 októbra 2007
Wolfram demonstrations
 Bohatým zdrojom zábavy a poučenia pre matematikov všetkých kategórií je projekt Wolfram demonstrations. Stačí si nainštalovať Mathematica Player a môžete začať so skúmaním približne 1800 interaktívnych programíkov. (Mathematica Player je zadarmo, avšak na vytvorenie vlastnej demonštrácie potrebujete program Mathematica, ktorý už zadarmo nie je. Je to trochu podobné ako Acrobat Reader a Acrobat.) Väčšina demonštrácií by si zasluhovala podrobnejší komentár a určite niektorím z nich venujem v budúcnosti celý príspevok, prípadne ich použijem na výuke. Ktoré demoštrácie zaujali najviac Vás?
Bohatým zdrojom zábavy a poučenia pre matematikov všetkých kategórií je projekt Wolfram demonstrations. Stačí si nainštalovať Mathematica Player a môžete začať so skúmaním približne 1800 interaktívnych programíkov. (Mathematica Player je zadarmo, avšak na vytvorenie vlastnej demonštrácie potrebujete program Mathematica, ktorý už zadarmo nie je. Je to trochu podobné ako Acrobat Reader a Acrobat.) Väčšina demonštrácií by si zasluhovala podrobnejší komentár a určite niektorím z nich venujem v budúcnosti celý príspevok, prípadne ich použijem na výuke. Ktoré demoštrácie zaujali najviac Vás?
28 septembra 2007
Zmeniť, či nezmeniť? To je otázka ...
Sme účastníci súťaže. Pred nami sú tri nepriehľadné krabičky, pričom vieme, že práve jedna z týchto krabičiek obsahuje hodnotnú cenu a zvyšné dve sú prázdne. Náhodne sme ukázali na jednu z týchto krabičiek a následne, v súlade s pravidlami súťaže, moderátor náhodne odstránil jednu prázdnu krabičku spomedzi zvyšných dvoch. (Samozrejme, medzi dvomi krabičkami, na ktoré neukazujeme, je aspoň jedna prázdna.) Po tomto sme dostali šancu zmeniť svoje rozhodnutie a vybrať si tú druhú krabičku, ktorá ešte zostala na stole. Má nejaký zmysel krabičku zmeniť, alebo nie?
27 septembra 2007
Nassim Nicholas Taleb: Fooled by Randomness
 "Realism can be punishing. Probabilistic scepticism is worse. It is difficult to go about life wearing probabilistic glasses, as one starts seeing fools of randomness all around, in a variety of situations - obdurate in their perceptional illusion."
"Realism can be punishing. Probabilistic scepticism is worse. It is difficult to go about life wearing probabilistic glasses, as one starts seeing fools of randomness all around, in a variety of situations - obdurate in their perceptional illusion." 26 septembra 2007
Rudyho ontológie
 Nasledovná klasifikácia ontológií je mierne modifikovaným a zhusteným zápisom myšlienok z knihy Rudyho Ruckera "The lifebox, the seashell, and the soul".
Nasledovná klasifikácia ontológií je mierne modifikovaným a zhusteným zápisom myšlienok z knihy Rudyho Ruckera "The lifebox, the seashell, and the soul".Definujme si nasledovné "množiny": V je množina všetkých procesov, ktoré sú výpočtom s konečným počtom pravidiel; M je množina všetkých procesov, ktoré je možné chápať ľudským rozumom; F je množina všetkých fyzikálnych procesov.
Zrejme budete súhlasiť s tým, že V<=F & V<=M (Pozri poznámku 1 a obrázok). Náš svetonázor je potom plne determinovaný jednou z nasledovných alternatív (v zátvorke sú Rudyho pomenovania a niektorí pravdepodobní prívrženci daných ontológií):
1. V=M=F (Universal automatism; Alan Turing)
2. V=M<F (Mechanism)
3. V<M=F (Physical antimechanism; Roger Penrose)
4. V<M<F (Common sense)
5. V=F<M (Supernaturalism)
6. V<F<M (Idealism; Kurt Gödel)
7. V=MF & V<M & V<F (Computationalism)
8. V<MF & V<M & V<F (Plentitude)
Ktorej z týchto možností najviac veríte? Svoju odpoveď môžete označiť v ankete v pravom stĺpci blogu. Poznámka január 2008: Anketa už skončila; výsledky si môžete pozrieť v samostatnom príspevku.
Poznámky: 1) Pre jednoduchosť budem značiť symbolom A<=B výrok, že množina A je podmnožina B, symbolom A<B výrok, že A je vlastná podmnožina B, t.j. existujú prvky B, ktoré nie sú prvkami A a symbolom AB prienik množín A a B. 2) Samozrejme, celá táto klasifikácia je vágna, pretože nevieme presne definovať ani jednu z množín V, M a F. Aj tak si však myslím, že dokážete aspoň intuitívne určiť, ktorý z uvedených ôsmich svetonázorov je ten Váš.
21 septembra 2007
Váženie dvanástich guličiek
 Máme 12 na pohľad identických guličiek, o ktorých vieme, že 11 z nich má rovnakú hmotnosť a jedna má hmotnosť inú (pričom nevieme, ktorá z nich to je a tiež nevieme, či je ľahšia, alebo ťažšia ako zvyšné guličky). Tiež máme k dispozícii klasickú váhu s dvomi miskami, ktorá vie ukázať len 3 rôzne výsledky: 1) Obsah ľavej misky je ťažší ako obsah pravej misky; 2) Obsah pravej misky je ťažší ako obsah ľavej misky; 3) obsah na oboch miskách je presne rovnako ťažký. Aký je najmenší počet vážení, ktorý nám umožní identifikovať, ktorá gulička je odlišná a aj určiť, či je ťažšia, alebo ľahšia?
Máme 12 na pohľad identických guličiek, o ktorých vieme, že 11 z nich má rovnakú hmotnosť a jedna má hmotnosť inú (pričom nevieme, ktorá z nich to je a tiež nevieme, či je ľahšia, alebo ťažšia ako zvyšné guličky). Tiež máme k dispozícii klasickú váhu s dvomi miskami, ktorá vie ukázať len 3 rôzne výsledky: 1) Obsah ľavej misky je ťažší ako obsah pravej misky; 2) Obsah pravej misky je ťažší ako obsah ľavej misky; 3) obsah na oboch miskách je presne rovnako ťažký. Aký je najmenší počet vážení, ktorý nám umožní identifikovať, ktorá gulička je odlišná a aj určiť, či je ťažšia, alebo ľahšia?20 septembra 2007
Najťažší elementárne formulovaný matematický problém ...
Nie je to tak dávno, čo Jeffrey Lagarias formuloval v reči elementárnych matematických operácií slávnu Riemannovu hypotézu. Stačí overiť, že pre všetky prirodzené čísla n je splnená nerovnosť
 (pričom rovnosť nastáva len pre n=1), ktorá zahŕňa len súčet kladných deliteľov čísla n, n-té harmonické číslo, prirodzený logaritmus a exponenciálnu funkciu; pozri priamo Lagariasov článok, alebo vzťah 5 na stránke mathworldu.
(pričom rovnosť nastáva len pre n=1), ktorá zahŕňa len súčet kladných deliteľov čísla n, n-té harmonické číslo, prirodzený logaritmus a exponenciálnu funkciu; pozri priamo Lagariasov článok, alebo vzťah 5 na stránke mathworldu.Drvivá väčšina matematikov verí, že Riemannova hypotéza je pravdivá. Avšak nie sú náhodou odsúdení len na večnú vieru a nič viac? Takýto zvrat sa Vám môže zdať trochu divný, ale matematika skrátka je veľmi podivná a asi si na to treba zvykať. Prečo?
O Gödelovych vetách ste už asi počuli, ale obvykle sa nám ich dopad zdá akosi vzdialený matematickej realite. Už dlhšiu dobu je však dokázané, že existuje nekonečne veľa Diofantických rovníc, ktoré nemajú žiadne riešenie v obore celých čísiel, ale pritom túto skutočnosť o nich nie je principiálne možné dokázať. Napríklad podľa Stephana Wolframa by takou rovnicou mohla byť m^2=n^5+6n+3. Úloha dokázať neexistenciu riešenia Diofantickej rovnice je pritom veľmi jednoducho formulovateľná a pomerne častá.
Takže tak. To čo je jednoducho formulovateľné a súčasne pravdivé, nemusí byť vôbec dokázateľné, aspoň nie v rámci našej bežnej formalizácie. Je teda možné, že aj Riemannova hypotéza je jednou z takýchto čudesných právd.
Poznámky: 1) Podobné proroctvá tu však boli už pred dokázaním veľkej Fermatovej vety a predsa sa nenaplnili. 2) Všetky moje komentáre týkajúce sa teórie čísiel a logiky berte trochu s rezervou; tieto oblasti sa mi páčia, ale nie som na ne expert. 3) Časť o Diofantických rovniciach je napísaná na základe knihy Rudyho Ruckera "The lifebox, the seashell, and the soul".
18 septembra 2007
Rudy Rucker: The Lifebox, the Seashell, and the Soul
 "I come to see the study of computation as the ultimate and most fundamental form of science, even more fundamental than mathematics."
"I come to see the study of computation as the ultimate and most fundamental form of science, even more fundamental than mathematics."Ak nechceme vynechať žiadny zamysleniahodný výrok z tejto knihy, tak je nemožné napísať recenziu stručnejšiu ako je táto kniha samotná. Rudy Rucker, bývalý profesor informatiky a aktívny autor science-fiction, spísal vo svojom magnum opus “The Lifebox, the Seashell, and the Soul” svoje názory na všetko od kvantovej mechaniky, cez vety o neúplnosti až po ľudské vedomie a zmysel života. Jednotiacou filozofiou Rudyho pohľadu na svet je “univerzálny automatizmus”, t.j. pohľad na všetky fyzikálne aj myšlienkové procesy ako na deterministický výpočet, ktorý je schopný produkovať akúkoľvek komplexitu, no pritom je popísateľný konečným počtom pravidiel. Pre Rudyho sú najzaujímavejšie výpočty, ktoré nazýva trochu podivínsky ako „gnarly”. Výpočty tohto typu sú nepredvídateľné, avšak vykazujú určitú štrukturovanosť, podobne, ako produkuje napríklad celulárny automat s pravidlom 30. Avšak viac ako kritický postoj vedca, cítiť z knihy autora science-fiction. Nadšený metaforou sa Rudy púšťa do odvodzovania často neprimerane ďalekosiahlych záverov. Napriek tomu som veľmi rád, že som si túto knihu kúpil a prečítal, pretože ma naučila dívať sa na niektoré veci z nového a veľmi zaujímavého "výpočtového" pohľadu, prípadne ma prinútila precíznejšie si zdôvodniť môj vlastný odlišný postoj.
Kľúčové slová: Turing machine, Conway's game of life, Post’s problem, Gödel’s incompleteness theorems, Mandelbort set, Zipf’s law, Wolfram’s New kind of Science
Poznámka: Pozri tiež príspevok "Rudyho ontológie".
