"Keď sa odborník na testovanie pozrie na rozdelenie úspešnosti z Testovania 9, okamžite mu musí udrieť do očí, že s grafom [pozri obrázok nižšie, v ľavej časti panelu, pozn. RH] niečo nie je v poriadku. Vyzerá o dosť inak, ako by mal. V čom spočíva jeho anomália? Gaussova krivka (ktorú samotný NÚCEM prikreslil do grafu) dáva odpoveď: žiakov s úspešnosťou 50 – 70 % je menej, ako by ich malo byť, a naopak žiakov s úspešnosťou 80 – 100 % je omnoho viac, ako by ich malo byť. S pravítkom a trochou trpezlivosti ľahko spočítate, že „posunutých smerom doprava“ (k vyššej úspešnosti) je viac ako 5 000 žiakov, teda viac ako 12 % testovanej populácie. Je pravda, že pri niektorých testovaniach môže byť výsledná Gaussova krivka posunutá smerom k maximálnemu skóre. K tomu však dochádza iba vtedy, keď je test pre danú skupinu žiakov príliš ľahký, čo tento rozhodne nebol – celková úspešnosť bola 60,07 %. A navyše: aj vtedy si krivka zachová svoj typický tvar. Človek nemusí byť Sherlockom Holmesom, aby mu bolo jasné, čo sa v Testovaní 9 stalo: výsledky nezodpovedajú skutočným vedomostiam žiakov z matematiky. Tie totiž naozaj majú Gaussovo rozloženie..."
Pripúšťam, že sa pri "Testovaní 9" mohlo podvádzať; pozrime sa však na samotný argument, ktorým pán Burjan svoje obvinenie podopiera. Musí výsledok testovania skutočne zodpovedať Gaussovej krivke?
Samozrejme, Gaussovo rozdelenie pravdepodobnosti je spojité rozdelenie s neohraničeným nosičom, zatiaľ čo výsledky testovania môžu nadobúdať len konečne veľa hodnôt, čiže tieto výsledky principiálne nemôžu zodpovedať úplne presnému Gaussovmu rozdeleniu. To je ale maličkosť; ide nám o to, či sa celkový tvar výsledkov testovania musí aspoň "podobať" na Gaussovu krivku.
Keby žiaci odpovede len tipovali, navzájom nezávisle, všetci rovnakým náhodným postupom (napríklad by si hádzali mincou pri vypĺňaní testu, v ktorom je pre každú otázku správna práve jedna z dvoch uvedených odpovedí), tak by sa výsledky na Gaussovo rozdelenie naozaj veľmi podobali. Matematické zdôvodnenie tohto javu poskytuje centrálna limitná veta. Lenže medzi úlohami sú rozdiely v náročnosti a najmä medzi žiakmi sú obrovské rozdiely v schopnostiach, čiže matematické predpoklady centrálnej limitnej vety jednoducho nie sú splnené a navyše celkové výsledky testovania budú "zmesou" rozdelení s veľmi rôznymi strednými hodnotami.
Pokúsme sa situáciu modelovať realistickejšie: Predpokladajme, že test pozostávajúci z 50 otázok absolvuje 40000 žiakov. Otázky však budú rozdielnej obtiažnosti: od 0 (veľmi ľahká otázka) až po 1 (veľmi ťažká otázka) a takisto žiaci budú mať v našom modeli rozdielne schopnosti: od 0 (veľmi slabý žiak) až po 1 (veľmi dobrý žiak). Predpokladajme, že riešenie úlohy môže byť len buď nesprávne, za 0 bodov, alebo správne, za 1 bod.
Pravdepodobnosť správneho vyriešenia úlohy závisí od náročnosti úlohy (túto náročnosť si označíme symbolom o) a taktiež od schopností žiaka (označíme si ju symbolom z). Ako jednoduchý rozumný model si stanovíme, že pravdepodobnosť správneho vyriešenia úlohy je
P=min(1,0.6+0.6(z-o)).
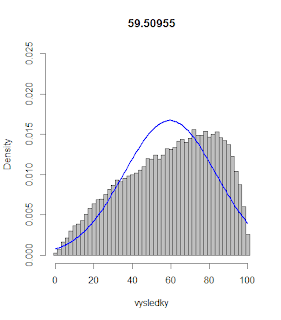
Tento vzorček znamená, že čím vyšší je rozdiel medzi schopnosťami žiaka a náročnosťou úlohy, tým je väčšia pravdepodobnosť správneho vyriešenia úlohy. V prípade, že je náročnosť úlohy rovnaká ako miera schopností žiaka, je pravdepodobnosť správneho vyriešenia úlohy 60 percent (toto číslo som zvolil po krátkom experimentovaní tak, aby sa stredná hodnota výsledku získaného z nášho modelu podobala na skutočný priemerný výsledok). Takto stanovený model je veľmi jednoduché nasimulovať (použil som krátky kód pre štatistický program R) a ... voilá!

Ako vidíme, výsledný histogram (sivé obdĺžničky) sa nielenže výrazne odlišuje od Gaussovho rozdelenia pravdepodobnosti (modrá krivka), ale dokonca až zarážajúco pripomína skutočné výsledky "Testovania 9".
Ukázalo sa teda, že argument pána Burjana založený na Gaussovej krivke nie je správny; už náš veľmi jednoduchý model dokazuje, že sumárne výsledky štátneho testovania nijako nenaznačujú, že pri ňom dochádzalo k "masívnemu" podvádzaniu. A NÚCEMu by som odporúčal, aby na budúce do histogramov výsledkov testovania Gaussovu krivku nedokresľovalo, lebo jej výpovedná hodnota je v takýchto situáciách sporná.
Ak sa Vás tento článok zaujal, podporte ho na vybrali.sme.sk .
Alebo, ak môžete, podporte našu fakultu v úsilí získať finančné prostriedky na opravu omietky našej budovy, ktorá nám nielenže padá na hlavu, ale aj odpudzuje potenciálnych študentov a pedagógov. (Samého sa ma snažili odlákať preč z matfyzu poukázaním na to, v akej ohyzdnej budove to pracujem. Ale nedal som sa. :)
Dodatok 14.5.: Nasimuloval som výsledky testu na základe matematickej formulácie Raschovho modelu a súčasne tak, že rozdelenie schopností žiakov je normálne. Zvolil som trochu nižšiu obtiažnosť otázok, aby bola stredná hodnota približne 60 percent maxima (ako v Testovaní 9) a po pár pokusoch som tiež odhadol vhodný parameter rozptylu schopností žiakov. Vyžiadalo si to len veľmi malú modifikáciu môjho pôvodného modelu a algoritmu, ako si môžete pozrieť. Program som spustil trikrát a dostal som nasledovné obrázky:
Ako vidíte, výsledky sa opäť zásadne odlišujú od gaussovského rozdelenia a navyše zhoda s výsledkami Testovania 9 je opäť dobrá, možno aj o niečo lepšia. Samozrejme, pre modely s viacerými parametrami by sa dal fit so skutočnými výsledkami testovania ešte zlepšiť. Tiež je zaujímavé si všimnúť, že pri rôznych spusteniach výsledný histogram značne "prirodzene" fluktuuje.
Sumarizácia toho na čo sme prišli (aj s pomocou niektorých veľmi kvalifikovaných čitateľov v diskusii; ďakujem):
1) Existujú jednoduché modely (ako napríklad ten Raschov), ktoré pre veľa nastavení parametrov dávajú výrazne negaussovské rozdelenie výsledkov a to aj pri nulovej miere podvádzania. Dokonca existujú také nastavenia parametrov, ktoré dávajú dobrú zhodu práve s výsledkami Testovania 9.
2) Komplexnejšie modely (ktoré by napríklad zohľadňovali to, že náročnosti a typy otázok môžu byť veľmi rôzne, kvalita študentov nutne závisí od celkového faktora úrovne školy, pričom školy majú veľmi rozdielne veľkosti a kvality) by celkom isto poskytovali priestor pre ešte komplikovanejšie formy výsledného rozdelenia. Nedá sa očakávať, že priblížením modelu realite by sa celková forma výsledkov začala približovať k jednoduchému gaussovskému rozdeleniu.
3) Simulácie naznačujú, že aj pri počte 40000 študentov výsledný histogram pomerne značne fluktuuje, čiže ľahko sa môžu v histograme výsledkov vyskytnúť rôzne zdanlivé anomálie; bolo by potrebné použiť podložené štatistické testy na kontrolu, či odchýlka od akéhokoľvek ideálu, ktorý niekto predpokladá, nemôže byť spôsobená len prirodzenou náhodnou fluktuáciou.
4) Empirické dáta taktiež jednoznačne ukazujú, že výsledky testovania majú často rozdelenie odlišné od gaussovského, najmä v prípade rozdielnej motivácie študentov dosiahnuť čo najlepší výsledok; je to skúsenosť viacerých pedagógov, ale aj výsledok niektorých rozsiahlych testovaní.
Z čisto vizuálneho porovnania ideálnej gaussovej krivky s výsledkami Testovania 9 sa preto nedá odvodiť taký silný záver, že sa pri ňom "masívne podvádzalo" a už vôbec nie vypočítať počet žiakov, ktorí podvádzali.
Samozrejme nie som naivný, aby som si myslel, že sa pri testovaní deviatakov vôbec nepodvádzalo. Verím tiež tomu, že pán Burjan toho o testovaní žiakov veľmi veľa vie (neporovnateľne viac ako ja), intuítívne možno správne vycítil, že s dátami nie je niečo v poriadku a keďže v jeho záujme je dobro pre naše školstvo, tak na problém možného podvádzania poukázal. Ale samotný argument a výpočet, ktorý použil na podporu tohto svojho presvedčenia, je založený na nesprávnom predpoklade.