Tanec molekúl

Keď som na Akadémii Trojstenu spomínal súvis Gaussovej krivky a objemov rezov mnohorozmerných kociek, napadlo ma, že by som rád vedel ako asi vyzerá "typická" množina ich vrcholov v dvojrozmernej projekcii. Včera večer som si teda v rámci oddychu napísal jednoduchý program, ktorý zobrazuje dvojrozmerné súradnice vrcholov pomaly rotujúcej mnohorozmernej kocky s farbami určenými súradnicami v ďalších troch rozmeroch.

Najprv som si myslel, že pre Vás vyrobím pomocou môjho programíku video, ale to by bolo nutne krátke. Rozhodol som sa preto dať Vám k dispozícii priamo zdrojový kód programu; stačí, keď si ho prekopírujete do R-ka a spustíte. Takto sa s ním môžete zabávať, vylepšiť ho podľa vlastných predstáv.

Prednáška na Akadémii Trojstenu

Ďakujem všetkým, ktorí ste sa zúčastnili mojej prednášky na Akadémii Trojstenu! Slidy k mojej tohtoročnej prednáške nájdete tu a slidy k mojej prednáške v roku 2007 nájdete tu. Boužiaľ, z prednášky nie je záznam a slidy sú len veľmi stručným náznakom toho o čom som rozprával, ale nevadí. Ak máte akékoľvek otázky, rád Vám na ne odpoviem.

Pôvodný text: Tento piatok (10.12.2010) bude na našej fakulte Akadémia Trojstenu; program si môžete pozrieť tu. Ak ste si klikli na odkaz, asi ste si všimli, že jednu prednášku mám ja. Trochu ma mrzí, že paralelne bude mať veľmi atraktívnu prezentáciu misof, pretože tú som si chcel pozrieť aj ja a to mi asi teraz nedovolia :). Predpokladám tiež, že o moju prednášku o Gaussovej krivke až taký veľký záujem nebude, takže ak ste sa aj na toto podujatie neregistrovali, ku mne do B-čka sa o 11:15 určite zmestíte...

Náhodný rez kocky

Zvolíme náhodne rovinu prechádzajúcu ťažiskom kocky ABCDEFGH.  S akou pravdepodobnosťou bude rez kocky ABCDEFGH touto rovinou šesťuholník?

Predpokladáme, že rovinu zo zadania volíme "rovnomerne" náhodne, čiže všetky orientácie tejto roviny sú rovnako pravdepodobné, alebo ešte presnejšie: jednotkový normálový vektor tejto roviny má rovnomerné rozdelenie na povrchu jednotkovej gule.

Poznámka 4.12.: Vídím, že táto úloha nikoho nezaujala, avšak ja osobne mám celkom radosť, že ma napadla. Na prvý pohľad sa totiž zdá ťažká, no v skutočnosti sa dá pomocou istých trikov z teórie pravdepodobnosti vyriešiť na niekoľko riadkov.

Tri trojuholníky

Problémy optimálneho navrhovania experimentov, čo je moja hlavná oblasť výskumu, sú prekvapivo pestré, pretože zasahujú do takmer všetkých matematických disciplín: od štatistiky a pravdepodobnosti, cez kombinatoriku, teóriu grafov, analýzu, lineárnu algebru, teóriu matíc, až po numerickú matematiku. Dnes sa mi pri písaní článku z tejto oblasti dokonca vyskytlo jednoduché tvrdenie z klasickej rovinnej geometrie; formulujme si ho ako úlohu.

Majme päť priamok p₁, p₂, q₁, q₂, q₃, ako je znázornené na obrázku, pričom priamky q₁, q₂, q₃ sú rovnobežné. Označme ako A_ij prienik priamok p_i a q_j. Dokážte, že súčet obsahov trojuholníkov A₁₁A₁₂A₂₃ a A₁₂A₁₃A₂₁ je rovný obsahu trojuholníka A₁₁A₁₃A₂₂.

Koľko matematikov, toľko dôkazov

Nasledovná jednoduchá, ale celkom pekná dôkazová úloha sa nám objavila pri písaní článku o optimálnom navrhovaní experimentov pre náhodné procesy. Spomenuli sme ju viacerým kolegom a každý prišiel po nejakom čase so svojim vlastným dôkazom. Som zvedavý, koľko rôznych dôkazov sa podarí nájsť Vám.

Ukážte, že ak hladká funkcia f:R→R spĺňa rovnicu

pre všetky reálne čísla x a všetky kladné reálne čísla δ, potom je f kvadratická funkcia.

Kvadratickou funkciu rozumieme aj lineárnu a konštantnú funkciu (s niektorými koeficientmi nulovými). Ako obvykle, symbol f ' označuje deriváciu funkcie f.

Konvexné smery

Nech f je reálna funkcia definovaná na množine všetkých dvojíc reálnych čísiel. Smerom nazveme každý vektor (u,v) jednotkovej dĺžky.  Budeme hovoriť, že funkcia f je konvexná v smere (u,v), ak pre každý bod (a,b) je konvexnou funkcia priradzujúca číslu α číslo f(a+αu,b+αv). Je zrejmé, že ak je funkcia f konvexná vo všetkých smeroch, tak je sama konvexná. Konvexnosť v jednom smere však samozrejme nestačí; napríklad nekonvexná funkcia f(x,y)=x²+y³ je konvexná v smere (1,0):

Stačí na zabezpečenie konvexnosti funkcie f konvexnosť v dvoch rôznych smeroch? V troch? ...

Aké je maximálne prirodzené číslo n, pre ktoré existuje nekonvexná reálna funkcia f  dvoch reálnych premenných, ktorá je konvexná v n rôznych smeroch (u₁,v₁), ... ,(u_n,v_n)?

Hlavolam z výstavy

Dnes som sa v rámci nedeľného oddychu vybral s manželkou a dcérkou do Slovenského národného múzea na výstavu "Matematika pre potešenie". Aj keď na prvý pohľad pôsobí táto výstavka pomerne chudobne, dá na nej celkom dobre zabaviť, čo platí dvojnásobne, ak máte so sebou dieťa :). Väčšina exponátov je založená na dobre známych princípoch, napríklad Galtonova skrinka, Buffonova ihla, Kreslenie grafu jedným ťahom, Möbiusov list, Tangram a podobne. Mňa najviac zaujalo vedro s mydlovou vodou, do ktorého bolo možné ponárať drôtené modely telies (napríklad kocka, pravidelný simplex, štvorboký ihlan) a sledovať tvar vzniknutých membrán, podobne ako v jednom našom staršom príspevku.

Výstavka obsahuje aj niekoľko hlavolamov, z ktorých sa mi jeden nepodarilo vyriešiť, hoci som nad ním strávil možno aj štvrť hodiny. (Trochu ma to rozladilo, pretože riešenie je určite veľmi jednoduché. :) Vy však možno budete úspešnejší ...

Poskladajte štvorec rozmerov 6x6 z ôsmich kúskov znázornených na nasledovnom obrázku.

How long will it take Marie to saw a board into 3 pieces?

K napísaniu tejto rekreačnej úlohy ma inšpiroval príspevok Math teacher fail na blogu TYWKIWDBI (credits: Lenka Filová). Za normálnych okolností, t.j. ak pod slovom "board" rozumieme obdĺžnikovú dosku, je odpoveď učiteľa nesprávna. Ale... :)

Márii trvá 1 minútu, kým rozpíli drevený útvar konštantnej hrúbky na 2 rovnaké časti. Ako dlho bude trvať Márii, kým rozpíli tento útvar na 3 rovnaké časti? Aké sú všetky možné "správne" odpovede v závislosti od tvaru tohto útvaru?

Uvažujeme len také útvary, ktoré je možné rozpíliť na dve aj na tri rovnaké časti a tiež predpokladáme, že Mária píli daný útvar najkratším možným rezom (alebo najkratším možným súčtom dĺžok rezov), po ktorom sa rozpadne na dve, resp. tri rovnaké časti. Na to, aby sme dve časti považovali za "rovnaké", nestačí, aby boli "zrkadlovo rovnaké" (povedzme, že strany dosky sú ofarbené rôznymi farbami, čo umožní rozlíšiť zrkadlovú podobnosť od skutočnej zhodnosti).

Kedy sa obsah rovná dĺžke

Nasledovná úloha ma napadla keď sme dnes písali zovšeobecnenie nášho článku o generovaní náhodných bodov na mnohorozmerných sférach. 

Množinu M v rovine nazývame hviezdicovo konvexnou, ak v nej existuje "centrálny" bod O, z ktorého je "vidieť" všetky body množiny M, čiže ak pre každý bod A množiny M platí, že úsečka OA je celá v množine M. Pre jednoduchosť budeme uvažovať len tie hviezdicovo konvexné množiny, ktoré sú ohraničené, a pre ktoré je centrálnym bodom bod O=(0,0).

Výsekom hviezdicovej množiny M určeným bodmi X,Y ležiacimi na hranici M nazveme útvar ohraničený úsečkami OX, OY a krivkou, ktorá tvorí hranicu množiny M medzi bodmi X a Y. (Na tomto mieste a aj ďalej predpokladáme, že sa pohybujeme od bodu X k bodu Y po hranici množiny M v "smere hodinových ručičiek"). Na ilustračnom obrázku je množina M modrá a výsek určený bodmi X,Y je červený:

Všimnime si, že kruh v rovine so stredom v O a polomerom 2 má nasledovnú vlastnosť: obsah výseku určeného hraničnými bodmi X,Y je presne rovný vzdialenosti bodov X a Y po hraničnej kružnici.

Otázka znie: Existujú aj iné hviezdicovo konvexné množiny M s vlastnosťou, že obsah výseku množiny M určeného hraničnými bodmi X a Y je rovný vzdialenosti bodov X,Y po hranici množiny M?

Poznámka: Nedefinovali sme síce presne, čo je to hranica množiny M a čo je to vzdialenosť hraničných bodov X,Y "po hranici", ale tieto pojmy by mali byť intuitívne dostatočne jasné na pochopenia jadra zadania, bez rozptyľovania sa exaktnými, no komplikovanými formálnymi definíciami.


16.8.: Riešenie úlohy nám do komentárov napísal Ivan. Stručne, množín s danou vlastnosťou je nekonečne veľa, napríklad ak dotyčnice ku hranici, všade tam, kde jednoznačné dotyčnice existujú, sú priamky vo vzdialenosti 2 od bodu O. Taká je aj nasledovná "hviezda" :)

Pochopiteľne, existuje mnoho ďalších otázok, ktoré by sme sa mohli spýtať, napríklad: 1) Je každá množina s uvedenou vlastnosťou prienikom a zjednotením systému polrovín určených priamkami vzdialenými o 2 od bodu O? 2) Aké množiny "s oblými hranicami", t.j. nie polygóny, majú túto vlastnosť? 3) Aké je zovšeobecnenie tejto úlohy do viacrozmerného priestoru?

Nočná pyramída o pravdepodobnosti a logike

Zajtra (v sobotu 29.5.) o 22:30 budem spolu s profesorom Anatolijom Dvurečenskim hosťom relácie "Nočná pyramída" Slovenského rozhlasu. Takže ak máte čas, budem veľmi rád, keď si nás vypočujete.

Pred pár hodinami som dostal scenár a je skutočne zaujímavý. Základné témy sú "teória pravdepodobnosti", "vzťah medzi matematikou a logikou", "možné svety" a "náhoda a nutnosť". Trochu je problém v tom, že väčšina (predbežných) otázok má buď komplikované, alebo dosiaľ neznáme odpovede, prípadne na ne odpoveď asi vôbec ani neexistuje... Ale o to väčšia zábava bude na ne odpovedať, takže sa na to veľmi teším :)

30.5.: Kompletný záznam relácie vo formáte mp3 si môžete stiahnuť na tejto adrese. Veľmi rád Vám odpoviem na akékoľvek (ďalšie) otázky k téme.

Éter v štvorrozmernom priestore

Minulý týždeň som konečne odovzdal habilitačnú prácu, odoslal som náš najnovší článok a navyše sa skončilo vyučovanie, takže sa opäť s radosťou vraciam k môjmu blogu :) Mali sme tu už viaceré úlohy z geometrie v rovine aj v priestore. Čo by ste ale povedali na úlohu z geometrie v hyperpriestore?

Predstavme si dvojrozmerných obyvateľov povrchu sférickej planéty, ktorá rotuje okolo svojej osi v nehybnom éteri. Títo obyvatelia síce nevedia vnímať tretí rozmer, ale pohyb povrchu svojej planéty voči éteru odmerať vedia. To znamená, že na istej do seba uzavretej priamke (z nášho pohľadu na rovníku planéty) pozorujú najvyššiu rýchlosť pohybu éteru a v dvoch špeciálnych bodoch (z nášho pohľadu na póloch) pozorujú nulovú rýchlosť pohybu éteru.

Moja otázka znie: Ak by náš trojrozmerný vesmír bol povrchom štvorrozmernej gule rotujúcej v nehybnom štvorrozmernom éteri a vedeli by sme odmerať relatívnu rýchlosť tohto éteru voči nám, ako by sme vnímali oblasti najrýchlejšieho pohybu éteru (čiže akýsi švorrozmerný rovník) a ako by sme vnímali oblasti nulovej rýchlosti pohybu éteru (čiže štvorrozmerné póly)?

Ekvidištantné permutácie

  Nech σ=(σ₁,σ₂,...,σ_n) je permutácia čísiel 1,2,...,n. Ak v rovine postupne spojíme body (σ₁,σ₂), (σ₂,σ₃),...,(σ_n-1,σ_n), (σ_n,σ₁) a (σ₁,σ₂), dostaneme euklidovský graf, ktorý permutáciu σ plne charakterizuje. Na nasledovnom obrázku sú znázornené grafy permutácií (1,3,4,2) a (1,2,5,6,3,4).

Všimnite si, že grafy na obrázkoch majú jednu zaujímavú vlastnosť: rovnakú dĺžku všetkých hrán. Otázka znie:

Existuje permutácia čísiel 1,2,...,n, kde n>6, ktorej graf má všetky hrany rovnakej dĺžky?

Reťaze z mincí

Pri príležitosti dňa čísla π som pre Vás vymyslel nasledovnú úlohu (tento krát pomerne jednoduchú :).

Na obrázkoch sú dve reťaze vytvorené z mincí. Ktorá z nich má väčší vnútorný obvod?

Pod vnútorným obvodom myslíme dĺžku hranice "mláčky", ktorá by vznikla, ak by sme medzi mince naliali vodu (samozrejme za predpokladu, že by tá voda pomedzi mince nepretiekla). Teším sa na Vaše riešenia.

Poznámka 16.3.: Túto úlohu je možné vyriešiť matematicky; nejde o skúšku Vášho vizuálneho odhadu.

Pozoruhodná potvora

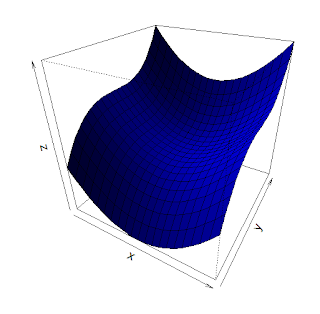
Matematické funkcie môžu mať veľmi komplikované vlastnosti, a to aj v prípade, keď sú definované jednoduchým predpisom. Včera mi pri riešení jedného príkladu vyskočila takáto pozoruhodná potvora:

 

kde λ je reálna konštanta. Čo všetko sa o nej dá povedať?

Po prvé si uvedomíme, že táto funkcia je dobre definovaná, pretože členy uvedeného nekonečného súčinu sú pre každé x od istého n v intervale (0,1), takže limita, ktorá určuje tento nekonečný súčin, existuje a je konečná. Tiež si hneď všimneme, že pre celé čísla x rôzne od nuly platí f(x)=0. Avšak prakticky akákoľvek ďalšia vlastnosť tejto funkcie je už netriviálna, ako naznačuje aj jej graf pre λ=1.5365:

Ak si niekto z Vás myslí, že je naozaj dobrý v matematickej analýze, môže sa pokúsiť zodpovedať napríklad nasledovné otázky:

• Je hodnota f(x) nenulová pre každé kladné neceločíselné x?
• Aká je množina tých hodnôt λ, pre ktoré je funkcia f ohraničená na celom R?
• Je derivácia tejto funkcie nenulová v každom bode x=2^k, kde k je celé nezáporné číslo?

A ak sa niekomu z Vás podarí zodpovedať na všetky tri tieto otázky do týždňa (samozrejme s rigoróznym dôkazom), tak mu darujem svoj The Princeton Companion to Mathematics, lebo tak bude pravdepodobne v lepších rukách ;-)

Timothyho úloha

V úvodnej časti knihy Princeton Companion to Mathematics uviedol Timothy Gowers ako príklad kombinatorickej úlohy nasledovné zadanie:

Koľko existuje nula-jednotkových matíc rozmeru n × n, ktoré majú v každom riadku aj v každom stĺpci maximálne dve jednotky?

Timothy sa neunúva dať na túto otázku odpoveď (zrejme je to pre neho príliš triviálne), ale normálnych smrteľníkov ako my môže takáto úloha celkom potrápiť. Priznám sa, že som nad ňou uvažoval skoro pol hodiny a nepodarilo sa mi odvodiť všeobecný vzorček; niekedy to človeku skrátka nezapne. Ale Vy budete možno úspešnejší...

Agátkina teória čísel

Dnes som s dcérkou (4,5 r.) absolvoval nasledovný rozhovor.

Agátka: Ako sa volá najväčšie číslo?
Ja: Najväčšie číslo neexistuje.
Agátka: Ty tomu nerozumieš tata. Najväčšie číslo existuje.
Ja: Áno? A aké je veľké?
Agátka: Ako milión takýchto skríň popísaných číslami.
Ja: Hm. A čo ak by si toto číslo zvačšila o jedna?
Agátka: Tak by som predsa dostala najmenšie číslo.
Ja: Najmenšie číslo?
Agátka: Áno. Jednotku. Čísla musia byť do kruhu.
Ja. Aha. A ak by niekto mal toľko koruniek, koľko je to najvačšie číslo a ja by som mu dal ešte jednu korunku, tak by mal koľko koruniek? Jednu?
Agátka: Ale tata. Keby mal niekto toľko koruniek, tak by bol nimi úplne zasypaný a nemohol by si mu dať už žiadnu korunku...

Nedosiahnuteľné body

Vo vnútri kruhu máme zakreslený bod A. Na hranici tohto kruhu zvolíme bod B, spojíme ho s bodom A úsečkou a stredom úsečky AB budeme kolmo viesť tetivu t. Uvažujme množinu tých bodov kruhu, ktorými tetiva t určite nemôže prechádzať, nech by sme B zvolili kdekoľvek na hranici kruhu. Čo všetko vieme o tejto množine bodov povedať? 

Poznámka 3.2.: Úlohu už prakticky vyčerpávajúco vyriešil Peťo a to dokonca vo všeobecnej, mnohorozmernej verzii; viď jeho blog.

Zbierka úloh z pravdepodobnosti je na svete

Po dlhom čase vymýšľania zadaní, počítania riešení, kontrol a editovania nám vyšla naša prvá kniha: Zbierka úloh zo základov teórie pravdepodobnosti. Hurá!

Zbierka obsahuje 519 úloh, z ktorých každá má uvedený aspoň číselný výsledok, a väčšina dokonca podrobný postup riešenia. Okrem rôznych príkladov na cvičenia, domáce úlohy a písomky, zaradili sme do nej aj viacero komplexnejších a zábavných úloh, napríklad klasiky ako Buffonovu ihlu a Buffonovo vlákno, úlohu o ruinovaní, Monty Hall problem, problém zberateľa kupónov, Banachove zápalky, dvojrozmernú náhodnú prechádzku a podobne, ale aj vlastné úlohy, ako napríklad úlohu o kurzoch stávkových kancelárií, nové úlohy o lámaní úsečiek, problémy počtov cyklov v náhodných permutáciách, úlohy týkajúce sa rozdelenia IQ v populácii a mnohé iné. Dúfame, že zaujmú.

Bohužiaľ, väzba knihy je dosť nevhodne zvolená a nekvalitne urobená (kniha sa dá len veľmi ťažko úplne roztvoriť a nebude sa z nej dať dobre kopírovať), ale za to už my, autori, nemôžeme. Každopádne, zbierka sa čítať dá a teraz nás už čaká len rozhodovanie, ako budeme našu zbierku rozdeľovať medzi ľudí a najmä akým spôsobom získame čo najväčšiu spätnú väzbu, aby sme vychytali chyby, lepšie vyvážili zadania a pripravili druhé vydanie :-)

Poznámka: Úlohy z prvej kapitoly si môžete pozrieť tu.

Fermatova množina

Dnes uplynulo presne 345 rokov od smrti slávneho Fermata a pri tejto príležitosti vyšiel na SME celkom pekný a čitateľsky úspešný článok. Diskusie k podobným článkom sú síce zaujímavé viac z psychologického, než z matematického hľadiska, avšak občas sa v nich vyskytne komentár, nad ktorým sa oplatí zamyslieť. V diskusii k článku o Fermatovi bola pre mňa takou nasledovná otázka čitateľa "toerotik":

"Ak mocnina 2 je Pytagorova veta, a pre [mocninu] 3 vraj mal [Fermat] dôkaz [veľkej Fermatovej vety], ako je to s mocninou napríklad 2,2?"

Teória čísiel nie je mojou silnou stránkou, ale tipol by som si, že táto otázka môže byť netriviálna aj pre špecialistu. Formulujme si preto nasledovnú, podstatne všeobecnejšiu úlohu:

Fermatovou množinou nazvime množinu všetkých reálnych čísiel r, pre ktoré existujú prirodzené čísla x,y,z spĺňajúce x^r+y^r=z^r. Čo všetko vieme povedať o Fermatovej množine?

Jedna z vlastností Fermatovej množiny je tá, že obsahuje čísla 1 a 2, ale neobsahuje žiadne väčšie prirodzené číslo (to je vlastne veľká Fermatova veta). Vieme povedať o nejakých ďalších reálnych číslach, že patria, alebo nepatria do Fermatovej množiny? Vieme povedať, či Fermatova množina obsahuje nekonečne veľa reálnych čísiel? ... Teším sa na Vaše postrehy.

13.1.: V komentároch sa nám podarilo dokázať, že Fermatova množina je hustá v reálnych číslach, čiže pri akomkoľvek reálnom čísle vieme nájsť ľubovoľne blízko nejaké číslo z Fermatovej množiny. Peťo tiež našiel pomerne nedávny článok, z ktorého plynie, že kladné čísla z Fermatovej množiny sú iracionálne, s výnimkou čísiel tvaru 1/n a 2/n, kde n je prirodzené číslo.

Napadlo ma, že by mohlo byť zaujímavé zobraziť grafy funkcií x^r+y^r-z^r reálnej premennej r pre niekoľko "malých" trojíc prirodzených čísiel x,y,z. Tu je výsledok pre všetky trojice prirodzených čisiel x,y,z, ktoré nepresahujú 8:

Červenou bodkou som zaznačil čísla r, v ktorých platí x^r+y^r-z^r=0, čiže čísla z Fermatovej množiny. Keď som zväčšoval počet trojíc x,y,z, červené bodky skutočne čím ďalej, tým hustejšie pokrývali množinu reálnych čísiel...