Zapadajúce množiny (súťažná úloha č.2)

Druhý príspevok do súťaže o najkrajšiu úlohu poslal Ondrej Budáč, študent 3. ročníka FMFI UK, odbor matematika.

Majme množinu M, ktorá obsahuje podmnožiny prirodzených čísel. Pre každé dva prvky A, B množiny M platí, že A je podmožina B, alebo naopak B je podmožina A. (Formálne povedané, M je úplne usporiadaná vzhľadom na inklúziu.) Môže sa stať, že množina M bude nespočitateľná?

Úloha je prevzatá; riešenie nájdete tu (pdf).

Sto väzňov (súťažná úloha č.1)

Prvú úlohu do našej súťaže poslal Ondrej Budáč, študent 3. ročníka FMFI UK, odbor matematika.

V miestnosti je sto krabičiek uložených v jednom rade. V každej je meno jedného zo sto väzňov (žiadni dvaja sa nevolajú rovnako) a meno každého väzňa je práve v jednej krabičke. Každý väzeň je vpustený dnu a môže sa pozerať do krabičiek, otvoriť ich môže však najviac 50. Po jeho odchode musí miestnosť ostať presne v takom istom stave, ako keď do nej vošiel. Ak sa každému väzňovi podarí nájsť jeho meno, tak sú všetci voľní. Väzni sa môžu na začiatku poradiť, ale potom ich odvedú na samotky a do miestnosti vodia postupne. Ako sa majú dohodnúť, aby maximalizovali šancu na úspech?

Ondrejov komentár: "Ak by sa väzni správali náhodne a navzájom nezávisle, je zrejmé, že šanca na priepustku je polovica umocnená na 100. Dá sa však vymyslieť postup, pri ktorom dostanú väzni priepustku s cca 30% šancou. Riešenie tejto úlohy sa dá celkom ľahko pochopiť, je veľmi elegantné a nápadité. O to ťažšie je na to dôjsť sám. Ja som to nevydržal a po polhodine uvažovania som si pozrel vzorové riešenie. Ale aj dosť veľké hlavy (kamaráti Česi na súťaži v Bulharsku a mnohí ďalší) si nad tým lámali hlavy a bezvýsledne..."

Úloha je prevzatá. Vzorové riešenie je uvedené na tejto stránke (pdf).

Čakanie dvoch na prvú trojicu

Príspevky do našej novej súťaže sa nejako nehrnú, tak som sa rozhodol Vás trochu inšpirovať nasledovnou úlohou:

Dvaja hráči sa dohodli na takýchto pravidlách: Na začiatku si každý hráč zvolí trojicu po sebe idúcich výsledkov hodu mincou, t.j. jednu z možností HHH, HHZ, HZH, HZZ, ZHH, ZHZ, ZZH a ZZZ, kde H znamená hlava a Z znamená znak. Vyhráva ten hráč, ktorého trojica sa pri hádzaní mincou vyskytne ako prvá. Napríklad ak si prvý hráč vyberie trojicu HZZ, druhý hráč trojicu ZZH a na minci padne postupne ZHZHHZHHHZZ, tak vyhráva prvý hráč, pretože trojica HZZ po sebe idúcich výsledkov sa pri hádzaní objavila skôr ako trojica ZZH. Hráč, ktorý si vyberá svoju trojicu ako druhý v poradí, si nemôže zvoliť rovnakú trojicu ako prvý hráč, avšak vie čo si prvý hráč vybral a tomu môže svoju voľbu trojice prispôsobiť. Otázka znie: Je táto hra spravodlivá pre oboch hráčov? Ak nie, ktorý hráč má výhodu?

Dodatok 21.11.: Rasťo už tento problém správne intuitívne odhadol a načrtol riešenie. Aby sme si vyjasnili aj detaily, nakreslil som nasledovný diagram (zodpovedajúci modelu situácie markovovským reťazcom):


Ako je možné z tohoto obrázka vyčítať, ktorú trojicu si má zvoliť druhý hráč v závislosti od toho, ktorú trojicu si zvolí prvý hráč?

Súťaž o najkrajšiu matematickú úlohu

Pred istým časom som Vám prostredníctvom miniankety položil otázku, či by ste mali záujem zúčastniť sa súťaže na blogu QED o najkrajšiu matematickú úlohu. Výsledky tejto ankety boli mierne optimistické, takže som sa rozhodol, že pôjdem do toho.

Stav súťaže k 20.3.: Do súťaže som už dostal všetkých 12 úloh; takže ďalšie už nie je možné posielať. Onedlho začneme vyberať víťaza.

Pravidlá súťaže: Aby ste sa do tejto súťaže zapojili, pošlite mi e-mailom tieto údaje:

• Vaše meno, alebo pseudonym*
• názov úlohy*
• presné znenie úlohy*
• zdroj úlohy* (vlastná/prevzatá)
• ilustračný obrázok
• doplňujúci komentár
• vzorové riešenie úlohy
• svoju www stránku
• ďalšie údaje o sebe, ktoré chce zverejniť

(Údaje s hviezdičkou sú povinné.)

Každý z Vás môže poslať maximálne 3 úlohy, ktoré publikujem tu na blogu QED ako samostatný príspevok. Vyhradzujem si však právo niektoré z nich zamietnuť, ak nedodáte povinné údaje, ak zadanie nebude spĺňať bežné štandardy kultivovaného textu a podobne.

Do súťaže prijmem prvých dvanásť úloh (hoci predpokladám, že kým sa také množstvo nazbiera, uplynie niekoľko mesiacov). Po uverejnení všetkých úloh vyzvem čitateľov, aby súťažné úlohy sami ohodnotili prostredníctvom ankety. Nie je nutné, aby ste boli Vy sami autorom Vami poslanej úlohy, ale originalitu budú ľudia určite hodnotiť pozitívne.

Víťaz dostane hodnotnú cenu - úplne novú, vyše 700 stranovú knihu Magic Universe z vydavateľstva Oxford University Press. Na stránkach books.google môžete do knihy Magic Universe aj nahliadnuť.

Bodkovaná guľa

V komentári k predchádzajúcemu príspevku navrhol Michal nasledovnú zaujímavú úlohu:

Koľko maximálne môžeme na nepriehľadnú guľu nakresliť bodiek tak, aby pre každú z týchto bodiek existoval smer pohľadu, z ktorého je vidieť len túto jednu bodku a žiadnu inú?

V zadaní predpokladáme, že z každého pohľadu vidíme celú polguľu aj s jej hranicou. Keďže pri takejto formulácii sa môžu vyskytnúť nejasnosti, uvediem aj nasledovné spresnenie.

Nájdite najväčšie prirodzené číslo n s vlastnosťou: Existuje 2n vektorov x₁,...,x_n,v₁,...,v_n v priestore R^m, m=3, spĺňajúcich


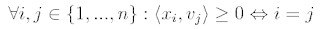
Alebo pomocou matíc:

Nájdite najväčšie prirodzené číslo n s vlastnosťou: Existujú matice X a V typu n×m, m=3, pre ktoré má matica XV^T všetky diagonálne prvky nezáporné a všetky mimodiagonálne prvky záporné.

Tento problém je síce ľahko zrozumiteľný, ale nie celkom triviálny. A ak by sa ho niekomu podarilo matematicky precízne vyriešiť pre ľubovoľnerozmernú guľu, resp. z pohľadu druhej a tretej formulácie pre všetky dimenzie m, tak klobúk dolu.

Dodatok 1 (3.11.): Ako poznamenal v komentároch Peťo, ľahšia sa zdá byť verzia b), ktorá vznikne zámenou neostrej nerovnosti vo formulácii 2 na ostrú nerovnosť, resp. zámenou slov "nezáporné" a "záporné" na "kladné" a "nekladné". V tejto verzii je jasné, že optimálne n je minimálne 2m.

Dodatok 2 (3.11.): Tak som to pre m=3 (t.j. pre klasickú guľu) vyriešil počas prechádzky s Aďkou a Agátkou na Partizánskej lúke a ukázalo sa, že ten problém vôbec nie je až taký ťažký. Práve naopak; riešenie by mohol nájsť aj bystrý žiak základnej školy! Ostáva však záhadou, ako je možné, že ma to riešenie napadlo až po asi hodine premýšľania... :-)