"Keď sa odborník na testovanie pozrie na rozdelenie úspešnosti z Testovania 9, okamžite mu musí udrieť do očí, že s grafom [pozri obrázok nižšie, v ľavej časti panelu, pozn. RH] niečo nie je v poriadku. Vyzerá o dosť inak, ako by mal. V čom spočíva jeho anomália? Gaussova krivka (ktorú samotný NÚCEM prikreslil do grafu) dáva odpoveď: žiakov s úspešnosťou 50 – 70 % je menej, ako by ich malo byť, a naopak žiakov s úspešnosťou 80 – 100 % je omnoho viac, ako by ich malo byť. S pravítkom a trochou trpezlivosti ľahko spočítate, že „posunutých smerom doprava“ (k vyššej úspešnosti) je viac ako 5 000 žiakov, teda viac ako 12 % testovanej populácie. Je pravda, že pri niektorých testovaniach môže byť výsledná Gaussova krivka posunutá smerom k maximálnemu skóre. K tomu však dochádza iba vtedy, keď je test pre danú skupinu žiakov príliš ľahký, čo tento rozhodne nebol – celková úspešnosť bola 60,07 %. A navyše: aj vtedy si krivka zachová svoj typický tvar. Človek nemusí byť Sherlockom Holmesom, aby mu bolo jasné, čo sa v Testovaní 9 stalo: výsledky nezodpovedajú skutočným vedomostiam žiakov z matematiky. Tie totiž naozaj majú Gaussovo rozloženie..."
Pripúšťam, že sa pri "Testovaní 9" mohlo podvádzať; pozrime sa však na samotný argument, ktorým pán Burjan svoje obvinenie podopiera. Musí výsledok testovania skutočne zodpovedať Gaussovej krivke?
Samozrejme, Gaussovo rozdelenie pravdepodobnosti je spojité rozdelenie s neohraničeným nosičom, zatiaľ čo výsledky testovania môžu nadobúdať len konečne veľa hodnôt, čiže tieto výsledky principiálne nemôžu zodpovedať úplne presnému Gaussovmu rozdeleniu. To je ale maličkosť; ide nám o to, či sa celkový tvar výsledkov testovania musí aspoň "podobať" na Gaussovu krivku.
Keby žiaci odpovede len tipovali, navzájom nezávisle, všetci rovnakým náhodným postupom (napríklad by si hádzali mincou pri vypĺňaní testu, v ktorom je pre každú otázku správna práve jedna z dvoch uvedených odpovedí), tak by sa výsledky na Gaussovo rozdelenie naozaj veľmi podobali. Matematické zdôvodnenie tohto javu poskytuje centrálna limitná veta. Lenže medzi úlohami sú rozdiely v náročnosti a najmä medzi žiakmi sú obrovské rozdiely v schopnostiach, čiže matematické predpoklady centrálnej limitnej vety jednoducho nie sú splnené a navyše celkové výsledky testovania budú "zmesou" rozdelení s veľmi rôznymi strednými hodnotami.
Pokúsme sa situáciu modelovať realistickejšie: Predpokladajme, že test pozostávajúci z 50 otázok absolvuje 40000 žiakov. Otázky však budú rozdielnej obtiažnosti: od 0 (veľmi ľahká otázka) až po 1 (veľmi ťažká otázka) a takisto žiaci budú mať v našom modeli rozdielne schopnosti: od 0 (veľmi slabý žiak) až po 1 (veľmi dobrý žiak). Predpokladajme, že riešenie úlohy môže byť len buď nesprávne, za 0 bodov, alebo správne, za 1 bod.
Pravdepodobnosť správneho vyriešenia úlohy závisí od náročnosti úlohy (túto náročnosť si označíme symbolom o) a taktiež od schopností žiaka (označíme si ju symbolom z). Ako jednoduchý rozumný model si stanovíme, že pravdepodobnosť správneho vyriešenia úlohy je
P=min(1,0.6+0.6(z-o)).
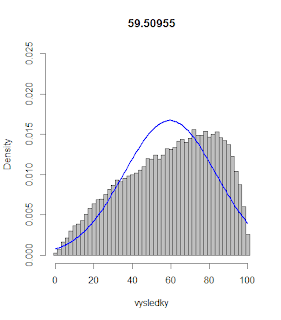
Tento vzorček znamená, že čím vyšší je rozdiel medzi schopnosťami žiaka a náročnosťou úlohy, tým je väčšia pravdepodobnosť správneho vyriešenia úlohy. V prípade, že je náročnosť úlohy rovnaká ako miera schopností žiaka, je pravdepodobnosť správneho vyriešenia úlohy 60 percent (toto číslo som zvolil po krátkom experimentovaní tak, aby sa stredná hodnota výsledku získaného z nášho modelu podobala na skutočný priemerný výsledok). Takto stanovený model je veľmi jednoduché nasimulovať (použil som krátky kód pre štatistický program R) a ... voilá!

Ako vidíme, výsledný histogram (sivé obdĺžničky) sa nielenže výrazne odlišuje od Gaussovho rozdelenia pravdepodobnosti (modrá krivka), ale dokonca až zarážajúco pripomína skutočné výsledky "Testovania 9".
Ukázalo sa teda, že argument pána Burjana založený na Gaussovej krivke nie je správny; už náš veľmi jednoduchý model dokazuje, že sumárne výsledky štátneho testovania nijako nenaznačujú, že pri ňom dochádzalo k "masívnemu" podvádzaniu. A NÚCEMu by som odporúčal, aby na budúce do histogramov výsledkov testovania Gaussovu krivku nedokresľovalo, lebo jej výpovedná hodnota je v takýchto situáciách sporná.
Ak sa Vás tento článok zaujal, podporte ho na vybrali.sme.sk .
Alebo, ak môžete, podporte našu fakultu v úsilí získať finančné prostriedky na opravu omietky našej budovy, ktorá nám nielenže padá na hlavu, ale aj odpudzuje potenciálnych študentov a pedagógov. (Samého sa ma snažili odlákať preč z matfyzu poukázaním na to, v akej ohyzdnej budove to pracujem. Ale nedal som sa. :)
Dodatok 14.5.: Nasimuloval som výsledky testu na základe matematickej formulácie Raschovho modelu a súčasne tak, že rozdelenie schopností žiakov je normálne. Zvolil som trochu nižšiu obtiažnosť otázok, aby bola stredná hodnota približne 60 percent maxima (ako v Testovaní 9) a po pár pokusoch som tiež odhadol vhodný parameter rozptylu schopností žiakov. Vyžiadalo si to len veľmi malú modifikáciu môjho pôvodného modelu a algoritmu, ako si môžete pozrieť. Program som spustil trikrát a dostal som nasledovné obrázky:
Ako vidíte, výsledky sa opäť zásadne odlišujú od gaussovského rozdelenia a navyše zhoda s výsledkami Testovania 9 je opäť dobrá, možno aj o niečo lepšia. Samozrejme, pre modely s viacerými parametrami by sa dal fit so skutočnými výsledkami testovania ešte zlepšiť. Tiež je zaujímavé si všimnúť, že pri rôznych spusteniach výsledný histogram značne "prirodzene" fluktuuje.
Sumarizácia toho na čo sme prišli (aj s pomocou niektorých veľmi kvalifikovaných čitateľov v diskusii; ďakujem):
1) Existujú jednoduché modely (ako napríklad ten Raschov), ktoré pre veľa nastavení parametrov dávajú výrazne negaussovské rozdelenie výsledkov a to aj pri nulovej miere podvádzania. Dokonca existujú také nastavenia parametrov, ktoré dávajú dobrú zhodu práve s výsledkami Testovania 9.
2) Komplexnejšie modely (ktoré by napríklad zohľadňovali to, že náročnosti a typy otázok môžu byť veľmi rôzne, kvalita študentov nutne závisí od celkového faktora úrovne školy, pričom školy majú veľmi rozdielne veľkosti a kvality) by celkom isto poskytovali priestor pre ešte komplikovanejšie formy výsledného rozdelenia. Nedá sa očakávať, že priblížením modelu realite by sa celková forma výsledkov začala približovať k jednoduchému gaussovskému rozdeleniu.
3) Simulácie naznačujú, že aj pri počte 40000 študentov výsledný histogram pomerne značne fluktuuje, čiže ľahko sa môžu v histograme výsledkov vyskytnúť rôzne zdanlivé anomálie; bolo by potrebné použiť podložené štatistické testy na kontrolu, či odchýlka od akéhokoľvek ideálu, ktorý niekto predpokladá, nemôže byť spôsobená len prirodzenou náhodnou fluktuáciou.
4) Empirické dáta taktiež jednoznačne ukazujú, že výsledky testovania majú často rozdelenie odlišné od gaussovského, najmä v prípade rozdielnej motivácie študentov dosiahnuť čo najlepší výsledok; je to skúsenosť viacerých pedagógov, ale aj výsledok niektorých rozsiahlych testovaní.
Z čisto vizuálneho porovnania ideálnej gaussovej krivky s výsledkami Testovania 9 sa preto nedá odvodiť taký silný záver, že sa pri ňom "masívne podvádzalo" a už vôbec nie vypočítať počet žiakov, ktorí podvádzali.
Samozrejme nie som naivný, aby som si myslel, že sa pri testovaní deviatakov vôbec nepodvádzalo. Verím tiež tomu, že pán Burjan toho o testovaní žiakov veľmi veľa vie (neporovnateľne viac ako ja), intuítívne možno správne vycítil, že s dátami nie je niečo v poriadku a keďže v jeho záujme je dobro pre naše školstvo, tak na problém možného podvádzania poukázal. Ale samotný argument a výpočet, ktorý použil na podporu tohto svojho presvedčenia, je založený na nesprávnom predpoklade.


35 komentárov:
Co sa testov tyka - nezalezi umiestnenie ("odrezanie") krivky normalneho rozdelenia aj od odhadnutia narocnosti testu ? V zmysle, ze lahky test sa bude podobat na "lavu stranu" krivky normalneho rozdelenia (ziaci, ktori by zvladli vysoke skore - tie male hodnoty "napravo" ostanu na nizsom skore, kedze test je jenoduchy.) (ak by toto aj bola pravda, pochopitelne to nie je jediny validny dovod, preco poctive vysledky nemusia kopirovat norm. rozdelenie)
V suvislosti s klucovymi slovami "podvadzanie" a "statistika" mi laicky napada pan Benford a jeho zakon, aj ked nevidim sposob, ako ho aplikovat v tomto pripade.
Jemne mimo temy: link na vybrali.sme.sk nefunguje a (minimalne mne) hlasovat sa neda.
samozrejme, ze deviataci podvadzali....ale rovnako aj stredne skoly pri externej casti....
Nie vsetky skoly , ale mnohe!A tiez im pri tom pomahali aj ucitelia:(
Niekde je tam chyba, pokial predpokladas ze schopnosti ziakov zodpovedaju normalnemu rozdeleniu, a dosiahnuty vysledok umerny schopnostiam (v tvojom pripade je umerny skor stvorcu schopnosti, ale to na veci meni len malo) vysledok stale pripomina normalne rozdelenie.
Tvoj kod ale predpoklada nahodne rozdelenie schopnosti v rozsahu 0 - 1, co je samozrejme zle a cela dalsia uvaha je zatazena touto chybou.
Co inac dobre ilustruje stav vzdelavania matematiky na Slovensku - naucene vedomosti, nepochopeny problem.
b314: Samozrejme umiestnenie Gaussovej krivky v tom grafe, čiže stredná hodnota daného normálneho rozdelenia, závisí od náročnosti testu. Aj v grafe od NUCEMu aj v mojom grafe je stredná hodnota toho Gaussovho rozdelenia určená priemerným výsledkom (a jeho smerodajná odchýlka je určená smerodajnou odchýlkou výsledkov). V tomto zmysle tá Gaussova krivka "fituje" dáta najlepšie ako môže. Ten link na vybrali.sme.sk som sa pokúsil opraviť.
liti: Je v podstate úplne isté, že k nejakému podvádzaniu dochádzalo. Článkom som chcel len povedať, že na základe porovnania celkových výsledkov s Gaussovou krivkou sa rozsah tohto podvádzania nedá odhaliť.
Peter Bozek: Ak by som modeloval schopnosti žiakov normálnym rozdelením, musel by som modelovať inak aj obtiažnosť otázok, resp. komplikovanejšie by som musel modelovať pravdepodobnosť, že žiak s danými schopnosťami vyrieši úlohu danej obtiažnosti. Takýchto modelov je pochopiteľne nekonečne veľa, každopádne všetky realistickejšie modely, ktoré zohľadňujú rôznu schopnosť riešiť matematické úlohy rôznymi žiakmi, budú vykazovať podobné správanie: rozdelenie výsledkov bude mať "menej špicatý vrchol" než má normálne rozdelenie. A ak bude mať výsledok vyššiu priemernú úspešnosť ako 50 percent, tak bude navyše to rozdelenie asymetrické. (Inak, na tom modelovaní schopností v rozsahu [0,1] nie je nič zlé ani len principiálne; pre akékoľvek {aj normálne} rozdelenie schopností žiakov existuje formulka určujúca pravdepodobnosť správneho vyriešenia úlohy, ktorá dá rovnaké výsledky ako dáva môj model. Interval, na ktorom sa náhodne generujú číselné hodnoty "schopností", je len vecou dohody.) Skrátka, akýkoľvek realistickejší model sa bude od Gaussovej krivky významne líšiť. Tú poslednú poznámku o stave vzdelávania na Slovensku som nepochopil; na čo narážate?
Pan Harman, vy ste si "vycucali z prsta" nejaky vlastny vzorcek popisujuci spravanie ziakov a z neho dalej nieco odvodzujete. Ten vzorec ma samozrejme kopu chyb a s realnym spravanim ziakov prilis nesuvisi. Tym padom je vsetko, co z neho vyplyva, irelevantne. Ja mam na rozdiel od vas k dispozicii stovky grafov rozdelenia hrubych skore zo skutocnych testovani tisicov a desattisicov ziakov a svoje argumenty opieram o empiricku znalost realnych dat. Mozno bolo nestastne pouzivat termin gaussova krivka, lebo to mnohych zvadzalo argumentovat, ze ta krivka nie je presne gaussova. Ano, nie je presne gaussova, ale rozhodne bez podvadzania nemoze vyzerat tak, ako vyzera. Mimochodom, ja som svoj povodny clanok uverejnil skor ako boli zverejnene zistenia inspekcie, ktore presne potvrdzuju to, co som povedal: ze na mnohych skolach sa podvadzalo. V. Burjan
Pekne si to napísal - argumentovať Gaussovou krivkou môže byť zaujímavé pre široké masy, pretože takýto pojem už niekedy počuli, ale pre skutočných matematikov je to trochu málo... Som rád, že si to tak pekne namodeloval (aj keď za cenu nejakých drobných nepresností, ktoré však principiálne nič nemenia na výsledku).
A k dátam - považovať vlastný komerčný produkt za reprezentatívnu vzorku nie je podľa mna vhodné ani správne (masovosť totiž nezaručuje reprezentatívnosť, keďže zaň treba platiť). Je to ale veľmi dobrý marketingový ťah - veľká publicita s nízkymi nákladmi...
Pán Burjan. Vytvoril som veľmi jednoduchý model toho ako súvisí pravdepodobnosť správneho zodpovedania otázky žiakom s obtiažnosťou otázky a schopnosťami žiaka. Je absolútne jasné, že tento model je len hrubým zjednodušením reality. Ale je to aspoň nejaký model, ktorý má zmysluplné kvalitatívne správanie, napríklad modeluje nerovnaké otázky a nerovnaké schopnosti žiakov tým, že čím je vyššia schopnosť žiaka, resp. nižšia obtiažnosť otázky, tým je väčšia pravdepodobnosť správnej odpovede (inak akú "kopu chýb" to vlastne obsahuje)? Navyše, simulácia ukázala, že výsledky tohto modelu až prekvapivo dobre zodpovedajú skutočným výsledkom testovania. Navyše, ja tým nikoho neobviňujem, okrem možno Vás, a aj to len z neopatrnosti pri argumentácii, nie z podvádzania.
Na druhej strane, Vy ste Vašu "analýzu" nepodložili úplne ničím, okrem nejakých vizuálnych podobností výsledkov iných testovaní (robených inými žiakmi za iných podmienok) s niečím, čo sa v hrubých rysoch ponáša na Gaussovo rozdelenie pravdepodobnosti a na základe toho obviňujete vo svojom časopise masy učiteľov a žiakov z podvádzania. Samozrejme pripúšťam (a stále to opakujem), že sa na tom testovaní mohlo masívne podvádzať. Ale Vaša *argumentácia*, na základe ktorej ste to akože odvodili (a tiež výpočet koľkým žiakom bol zlepšený výsledok), je vyložene nesprávna.
ja inac tiez nechapem, preco by malo byt vysledne rozdelenie podobne gaussovke.
na http://www.nucem.sk/documents//26/testovanie_9_2012/vysledky/T9_2012_vyhodnotenie_pdf.pdf su vysledky z minuleho roku a su tam tiez grafy rozdelene podla znamky, aku ziaci dostali na polroku... tomu by som viac veril, ze sa bude podobat na gaussovku (ak si predstavime, ze bodovy zisk ziaka je nahodna premenna, tak aspon scitavame n.p. s podobnou ocak. hodnotou - ale aj tak, CLT predpoklada iid premenne)
ak sa ale scita 5 takychto kriviek, nemusi to byt gaussovka
otazka: co sa vie o nejakych slabsich postacujucich podmienkach (slabsich ako CLT), aby vzniklo daco "podobne" ako gaussovka?
Rado, uplne si to vystihol ked si konstatoval ze realnejsi model by musel byt omnoho zlozitejsi. Skusim tu naznacit ako by mal vyzerat: Nech N(iq) je normalne rozdelenie ziakov podla inteligencie (specifickej formy inteligencie ktora sa prejavuje schopnostou riesit matematicke problemy, aby sme boli presni) a nech V(iq) je priemerny vysledok ktory v teste ziak s s danym iq dosiahne. V(iq) je zrejme monotonna rastuca funkcia.
Potom vysledny graf bude mat tvar N(iq).V(iq) pre zavislost poctu bodov na iq respetive N(V(^-1)(n)) pre zavislost poctu ziakov na vysledku (kde N(^-1) je inverzna funkcia, ktora tiez musi byt monotonna rastuca - toto pisem len tak z hlavy, ale myslim ze to je jasne) a ked trochu poexperimetujes s roznymi funkciami pre V, zistis ze - prave kvoli monotonnosti V, resp. jej inverznej funkcie - je vysledna funkcia stale velmi pripominajuca normalne rozdelenie.
To by ti ale ako matematikovi malo byt uplne jasne, a prave na to som narazal ked pisal o urovni vzdelavania na slovensku - zda sa mi ze sa u teba prejavuje Kruger-Dunningov efekt v plnej krase.
Veľmi pekný príspevok kolegu Harmana. Dokonca by možno stálo za to preveriť, či Harmanov model až moc dobre nefitol schopnosti žiakov merané v tomto teste. Na druhej strane ma zaráža až neprimeraná arogancia pána Burjana, ktorý absolútne bez argumentu dáva silné vyhlásenia. Myslím tým aroganciu v reakcii na príspevok R.H. Neuprieram V. Burjanovi expertnú skúsenosť správne vycítiť kedy došlo k podvádzaniu na testoch. To ale nič nemaní na fakte, že R.H. veľmi správne a vecne poukázal na to, že tvrdenie o podvádzaní proste nie je oddôvodniteľné spôsobom o aký sa pokúsil V. Burjan. Odporúčam zapísať si tabuľku pravdivostných hodnôt implikácie a trocha sa nad ňou zamyslieť. :) Michal Demetrian
Pre Peter Bozek:
ja tu nebudem urazat ostatnych ako to robite Vy - ale skuste sa zamysliet nad tym co napisal pan Harman a aky statisticky model pouzil a ze aj ked nie je uplne realny tak podla mna viac vystihuje realitu... Vela veci moze dopredu zvadzat na Gaussa, ale moze byt viac veci co to zmenia. V tomto pripade ak sa uroven otazok znizi alebo zvysi tak to Gaussa moze rozhodit ...
kuko: Klasická centrálna limitná veta (CLV) obsahuje predpoklad nezávislosti, ako aj predpoklad rovnakého rozdelenia postupnosti náhodných premenných. Oba tieto predpoklady sa dajú istým spôsobom oslabiť tak, aby sa zachovala normalita limitného rozdelenia štandardizovaného priemeru. Čo sa týka oslabenia predpokladu rovnakého rozdelenia, najznámejšia je takzvaná Ljapunovova podmienka, ktorá istým spôsobom ohraničuje centrálne momenty vyššieho ako druhého rádu daných náhodných premenných. Ešte slabšia podmienka zabezpečujúca asymptotickú normalitu štandardizovaného priemeru je takzvaná Fellerova-Lindenbergova podmienka. O rôznych formách CLV sa toho vie veľmi veľa a sú jej venované celé hrubé knihy.
Rado, rozumiem co pises ale myslim ze na to ides matematicky z nespravneho konca. Ty ani ja nemame model ako sa to sprava. Ty argumentujes ze vies vytvorit model podla ktoreho dostanes podobne rozdelenie bez toho aby sa podvadzalo. Ale to sa v matematike da skoro vzdy a nie je to pointa. Lepsia cesta je v praxi zobrat to z druheho konca. Pozri sa na distribucie podobnych testov. Ak sa ta distribucia nepodoba je tam nejaky problem. Najpravdepodobnejsie vysvetlenie vyzera byt ze sa bud podvadzalo alebo bol ten test moc lahky. V obidvoch pripadoch bol ten test zly. Ak ta distribucia nie je kompatibilna ani s distribuciou lahkych testov, je spravne predpokladat ze sa podvadzalo. Ja som nevidel vysledky stoviek testov ale pan Burjan ich videl. Je to ako ked ti expert povie ze nieco nesedi a ty prides bez skusenosti s modelom ze mozno je vsetko ok. Je to trochu naivne. Myslim ze to co pise pan Burjan treba brat vazne, overit ci sa naozaj podvadzalo a ak ano, vyhodit vsetkych ucitelov a riaditelov co sa na tom podielali. S tym myslim suhlasime obaja.
Napríklad na stránke http://ibobor.sk/vyhodnotenie2012.php je vidieť nejaké testy a od Gaussa majú ďaleko. A nemyslím si, že sú jediné. Jano Žabka
Peter Bozek: Dobre, poďme si ten Váš model vyjasniť. Píšete, že "Nech N(iq) je normalne rozdelenie ziakov podla inteligencie". Normálne rozdelenie ako matematický objekt je pravdepodobnostná miera na množine reálnych čísiel, nie funkcia reálneho argumentu, takže predpokladám, že N má označovať *distribučnú funkciu* normálneho rozdelenia (zrejme to nemala byť *hustota*, pretože tá sa takým spôsobom ako píšete netransformuje; ak som Vás v niečom nepochopil, tak ma prosím opravte). Píšete, že ak V(iq) je monotónne rastúca funkcia, vyjadrujúca závislosť priemerného bodového zisku na IQ žiaka, tak "N(V(^-1)(n))" vyjadruje závislosť počtu žiakov na výsledku. Keďže N nadobúda len hodnoty v intervale (0,1), tak zrejme ste mali na mysli tvrdenie, že "N(V(^-1)(n))" je distribučná funkcia priemerného bodového zisku žiakov.
Zvoľme teda za V päťdesiatnásobok distribučnej funkcie práve normálneho rozdelenia IQ žiakov, čiže položme V=50*N. Takto definované V je krásna monotónne rastúca sigmoidálna funkcia, ktorá nadobúda hodnoty v intervale (0,50) bodov a mimochodom takéto funkcie sa naozaj bežne používajú na vyjadrenie závislosti nejakej ohraničenej premennej na potenciálne neohraničenej nezávislej premennej. Pre jej inverznú funkciu platí $V^{-1}(n)=N^{-1}(n/50), n \in (0,50)$, takže $N(V^{-1}(n))=N(N^{-1}(n/50))=n/50, n \in (0,50)$, čo je distribučná funkcia *rovnomerného* rozdelenia na množine bodov, ktoré je ešte oveľa vzdialenejšie gaussovskému rozdeleniu ako to, ktoré vyšlo z mojich simulácií. Ejha, zdá sa, že ten Váš model skôr potvrdzuje, a nie vyvracia to, čo tvrdím v blogovom príspevku.
A čo sa týka toho Dunningovho-Krugerovho efektu, ten poznám; voľne povedané, nekvalifikovaní ľudia preceňujú svoje vedomosti v danej oblasti a, naopak, kvalifikovaní ľudia preceňujú vedomosti ostatných v danej oblasti. Nemusíte sa obávať pán Bozek, je som si dobre vedomý, že v takýchto verejných diskusiách sa musím baviť o veciach z môjho odboru s rôznymi truhlíkmi, pričom nijako zvlášť nepreceňujem ich schopnosti.
Ak vas zaujimaju funkcie, akymi sa skutocne modeluju ziacke odpovede v testoch, precitajte si nieco o parametrickych logistickych modeloch najznamejsi je 1-parametricky Raschov model) a porovnajte ich zlozitost s vasim jednoduchym vzorcekom. Trvam na tom, ze z vasho arbitrarneho vzorca, ktory ste nicim nepodlozili, nemozete nic vyvodzovat. Mne vycitate, ze som nedal dostatocne argumenty pre svoje tvrdenia. A ake ste dali vy argumenty, ktorymi by ste nas presvedcili, ze vas vzorec nejako suvisi s realitou? Mozno bola chyba, ze som v clanku pouzival pojem Gaussova krivka. Mozno som to mal proste napisat jednoducho takto: 20 rokov sa zaoberam testami, videl som rozlozenia vysledkov stoviek testov. Som v danej oblasti expertom a jednoducho vidim, ze taky graf, aky NUCEM publikoval, nemoze vzniknut bez podvadzania. Vam, ako matematikom, by samozrejme takato argumentacia nestacila, ale, uprimne, mojim cielom nie je presviedcat matematikov. V. Burjan
Juro: Samozrejme, že nemáme a nikdy nebudeme mať presný model na to ako prebieha testovanie žiakov, pretože je to enormne komplikovaný proces zahŕňajúci tisíce ľudí. Lenže úplne presný model na správanie sa niečoho reálneho nemáme vo vôbec žiadnej oblasti vedy (s možnou výnimkou niektorých najfundamentálnejších fyzikálnych teórií). Dá sa povedať, že na nie celkom presných modeloch stojí podstatná časť celej vedy. Ide o to, že aj nie celkom presný model nám môže poskytnúť vhľad do toho, ako sa "správa realita" (prípadne nám poskytne predikcie) a práve to sa stalo pri tomto mojom modeli. A nie je pravda, že na akýkoľvek vopred požadovaný výsledok vieš nájsť kvalitatívne správny približný model, ktorý by tento výsledok podporoval.
(Inak, aj z pragmatického hľadiska je použitie približných modelov užitočnejšie, ako keď nepoužijeme žiadny model. Napríklad modely, ktoré používajú poisťovne, sú tiež len hrubým zjednodušením reality, dokonca aj fyzikálne modely, na základe ktorých NASA dopravilo človeka na Mesiac, neodrážajú realitu úplne presne).
Súhlasím s tým, že dlhoročné skúsenosti pána Burjana sú veľmi dôležité a je možné, že na ich základe správne vycítil, že s výsledkami testovania nie je niečo v poriadku. Ja si tiež myslím, že chce dobre, že na to, aby sa nepodvádzalo, treba dôsledne dbať, podozrenia z podvádzania treba preverovať a ak sa dokážu, tak je správne zodpovedných za to postihovať.
Ja v mojom príspevku netrvdím nič iné, len že jeho *zdôvodenie* svojho podozrenia odlišnosťou výsledkov od gaussovej krivky nie je správne, pretože existuje veľmi jednoduchý pohľad na vec, ktorý pripúšťa pozorované výsledky aj za predpokladu, že sa nepodvádzalo.
Možno som mal uviesť ešte jednoduchší model ako je ten v blogovom príspevku. Rozdeľme školy na "slabé", "priemerné" a "dobré". Aj ak predpokladáme, že výsledky žiakov zo slabých škôl majú normálne rozdelenie, aj výsledky žiakov z priemerných škôl majú normálne rozdelenie, aj výsledky žiakov z dobrých škôl majú normálne rozdelenie, tak je zrejmé, že priemerné výsledky v týchto typoch škôl budú veľmi odlišné (budú zodpovedať trom odlišným gaussovským krivkám). Sumárne výsledky všetkých žiakov dokopy teda budú zmesou troch gaussovských kriviek a tá zmes môže mať veľmi ďaleko od klasickej (jednej) gaussovskej krivky. V skutočnosti je celé "kontinuum" kvalít škôl a kvalít študentov, každopádne zmes výsledných navzájom poposúvaných rozdelení, aj ak by každé z nich bolo gaussovské, nezodpovedá gausovskému rozdeleniu. Práve naopak, bude opäť potvrzovať kvalitatívny uzáver z môjho modelu, že sumárne výsledky budú mať "sploštenejší tvar" v porovnaní s gaussovským rozdelením.
Fúha, to je hodín, dnes už musím seriózne pracovať, takže prípadné pokračovanie diskusie až zajtra. :)
Jano Zabka o nieco vyssie pise:
"Napríklad na stránke http://ibobor.sk/vyhodnotenie2012.php je vidieť nejaké testy a od Gaussa majú ďaleko. A nemyslím si, že sú jediné."
Ja pouzivam pojem Gaussova krivka sirsie ako matematici a pre mna je aj tento graf Gaussovou krivkou, i ked mierne deformovanou, pretoze test bol pre ziakov tazky. Ale je to presne tak vyzerajuci graf, ako MA vyzerat graf tazsieho testu. A ak si urobis zrkadlovy obraz toho grafu, dostanes ukazku toho, ako MA vyzerat graf lahkeho testu. A potom porovnaj ten zrkadlovy obraz s grafom z Testovania 9. Vidis ten rozdiel? Ide o tvar tej krivy, o to, ako pada smerom dolu na "hornom konci". O pocet inflexnych bodov... Proste vyzera inak. A ta z Bobra je OK.
Rado, ja rozumiem co pises. Ale mam iny nazor. Robim s datami a nemyslim si ze mat model je vzdy lepsie. Dokonca ani u poistovni. Popularna kniha kde je argument preco to je nespravne je Taleb - Antifragile. Ale spat k teme: podla mna spravny postup je sa najprv pozriet na podobne testovania, nie vymyslat model. Ak distribucia nesedi s predchadzajucimi testami tak tam proste skoro isto je nieco zle. Moj laicky pohlad na tu krivku je ze cast ziakov bola prelozena z normalnej distribucie do "umele zlepsenej distribucie". Tam kde ta krivka ma padat dole naraz zacne stupat. Co je zvlastne ked ten test mal viacero nezavislych otazok. Vzdy je mozne ze mala cast deti su geneticky vylepseni x-meni a tvoria tu druhu krivku, ale to by museli zmutovat naraz od toho posledneho testu z normalnou distribuciou. ;-) Ale nechcem spekulovat a naozaj v testovani by som sa skor spolahol na to co pise pan Burjan. Ked niekto videl realne data a vyzna sa v tom tak to myslim zavazi viac ako teoreticke modeli. Pan Burjan sa tym zaobera vela rokov a na Slovensku myslim skusenejsieho cloveka v tejto oblasti nenajdes. Ale paci sa mi co pises, je to sranda o tom diskutovat, len realita je bohuzial asi ze sa totalne podvadza a deti sa v skole ucia nie len matematiku. Po tom sa myslim niet co cudovat ze sa podvadza vsade.
Som laik, ale - Na tom odkaze i-bobor je krivka "kadeti 2012/2013 rozdelenie poctu bodov" s podobnym dvojitym vrcholom. Podvadzalo sa azda aj tam ?
Juro: Co sa tyka "superskupiny" - nemusia to byt "geneticki vylepseni x-meni" ale aspon ciastocne by to teoreticki mohli byt napr. ziaci "elitnych skol" ktore naucia viac a lepsie. Ale nevylucujem ze take na Slovensku (takmer?) neexistuju.
Roni, model ktory Rado pouzil nevystihuje realitu vobec - schopnosti ziakov nie su rovnomerne rozlozene v nejakom intervale, ale maju tvar normalneho (Gaussovskeho) rozlozenia okolo nejakej strednej hodnoty. Ak by do svojho modelu dosadil realisticky predpoklad normalneho rozdelenia schopnosti ziakov, dostane gaussovske rozdelenie krivky uspesnosti.
Dobre, urobil chybu a chyby robi kazdy - to nie je problem. Problem je v tom ze aj ked uznal ze jeho model nie je realisticky, tvrdi ze kazdy model bude vyzerat podobne. Tu uz robi to co vytyka Burjanovi - tvrdi nieco co nepodlozil (a nie je to ani pravda, co asi vie), a pokial Burjan sa moze opriet o empiricke udaje, Rado sa nemoze opriet o nic.
A BTW, v realnom zivote empiricke udaje prebijaju kazdu teoriu, o chybnej nehovoriac. Obvinit niekoho ze jeho argumentacia je nespravna, pretoze vychadza z empirickych udajov, je podla mna viac nez chybne, je nepochopenim vztahu medzi udajmi a teoriou - a to ma viedlo k tym poznamkam o urovni slovenskeho vzdelavania. Produkuje ludi co si myslia ze vedia viac nez vedia - odtial referencia na Kruger-Dunninga.
Takze IMHO ja sa spravam k Radovi miernejsie ako on k Burjanovi, omnoho ostrejsie slova by boli plne ospravedlnitelne.
Jeden pekny priklad na ilustraciu. Vedenie nasej fakulty od nas vlani chcelo, aby sme testovali "kvalitu" nasho vyucovania tak, ze na zaciatku a na konci semestra zadame studentom test z vyucovanej problematiky. Studenti teda vyplnovali takmer rovnaky test na zaciatku a na konci semestra. Vo vsetkych skupinach, ktore som testovala mali vysledky prveho testu, v ktorom studenti nevedeli odpovedat na otazky, tvar normalneho rozdelenia (vizualne). Ti isti studenti na konci semestra (s dostatocnou motivaciou riesit ulohy spravne) vytvorili pri rieseni testu rovnakej obtiaznosti znacne negaussovske rozdelenia.
Ako ich ucitel si myslim, ze to nebolo kvoli tomu, ze podvadzali, ale kvoli tomu, ze tentokrat nevyberali odpovede nahodne.
A dakujem za krasny priklad vyuzitia statistiky v realite.
Problem vasho mdoelu je ze v R kode ste pouzili funkciu runif() na generovanie "inteligencie ziaka". Tato funkcia vsak generuje nahodne cisla v intervale 0 az 1. ktore nie su normalne distribuovane okolo 0.5. Inteligencia ziakov je vsak distribuovana podla normalnej distribucie.
ked si vas kod zbehnete este raz a miesto runif() pouzijete funciu ktora generuje cisla normalne distribovane okolo 0.5, vysledok bude tiez normalne distribuovany....
Rado, v svojom tvrdeni "Práve naopak, bude opäť potvrzovať kvalitatívny uzáver z môjho modelu, že sumárne výsledky budú mať "sploštenejší tvar" v porovnaní s gaussovským rozdelením." zase robis rovnaku chybu. Totiz ak predpokladas ze (pociatocne) schopnosti ziakov maju normalne rozdelenie, a urovben skol ma normalne rozdelenie, tak aj vysledna uroven ziakov bude mat normalne rozdelelenie.
Laicky, ak by to tak nebolo, tak takmer ziaden jav by nemal normalne rozdleenie, pretoze kazdy je vysledkom roznych posobeni.
Cim chcem povedat je normalne rozdelenie je to co sa da cakat - preto sa nakoniec tak vola - ak vysledok tomu nezodpoveda, tak treba hladat preco. Je zrejme (aspon pre mna) ze nerealny priklad nie je takym vysvetlenim, podvadzanie mozno tiez nie, ale chce to iny dovod (ako nerealny priklad.)
Tvoja predstava ze realny system sa bude nejak podobat systemu ktory je zalozeny na chybnom - alebo nerealnom, ked to tak chces nazvat, ale ide o chybny predpoklad - je zakladna chyba ktoru stale opakujes.
BTW, na podvadzanie poukazuje viac indicii nez len tvar krivky - napriklad skok pri 90% uspesnosti, pricom (ako som cital) 90% zarucovalo postup na strednu skolu bez prijimacok? Nie je to naznak ze ucitelia systematicky pomahali ziakom prejst cez tuto hranicu?
Otazocka:
Ak pri uplne nahodnom vybere odpovedi je vysledkom gaussova krivka...
... a pri skutocnom teste (ak ziaci nepodvadzaju) ma byt vysledkom tiez gaussova krivka...
...aky ma vlastne zmysel studovat? :)))
Ešte k tomu ibobrovi:
http://ibobor.sk/vyhodnotenie2012.php
Konkrétne graf KADETI predsa nemá ani počet inflexných bodov rovnaký ako Gauss...
Navyše, to, že sa niečo PODOBÁ na Gaussovu krivku ešte neznamená, že to aj Gaussova krivka je. Ak to niekto používa širšie - asi tým myslí podobnosť tvaru - mal by vedieť, že potom na základe podobnosti tvaru nemôže dopočítať, že 12 % žiakov podvádzalo. Lebo výpočet by sedel, keb to bola Gaussova krivka a nie sa na ňu iba podobala.
Ďalšie grafy z iných testovaní (z diskusie na SME):
http://i.imgur.com/ZR4jdWt.png
A okrem nich som za posledné dva dni videl toľko grafov z testovaní všelijakého druhu, že už aj tá empíria ma prekvapuje, lebo som videl viac negaussov ako Gaussov.
Jano Žabka
Tu je diskusia k obrazku ktory poslal pan Zabka. Vcelku sranda.
http://www.reddit.com/r/dataisbeautiful/comments/1bqf9r/unusual_distributions_of_scores_on_final/
ked som pozeral tie polske obrazky uvedomil som si ze to je vysvetlenie - pokial jazykove testy maju pekny nornalny priebeh, matematicke nie, a pritom by to malo byt naopak. Dovod je (pravdepodobbne) jednoduchy - v pripade jazykovych testov doslo k zmene hodnotenia pri hodnoteni (ako je to tam vysvetlene) a to len pre prejdenie cez test, ale v pripade matematiky dochadza k podvadzaniu v priebehu testu - pokial ziak (alebo ucitel) nemoze druhemu vypracovat slovnu ulohu, moze mu prezradit vysledok.
v slovenskom pripade zrejme skoly samotne vyhodnocovali testy, tak je tam vidiet vplyv obidvoch podvodov - krivka je zdeformovana a zaroven je tam skok na 90%
Ďakujem veľmi pekne za pozitívne komentáre aj za konštruktívnu kritiku! Bohužiaľ, nebudem mať čas reagovať na každý z nich individuálne, pretože mám teraz veľmi náročné obdobie v práci (a o pár dní cestujem na konferenciu do Talianska). Zareagujem len na niektoré z nich.
Pán Burjan: Pozrel som si matematickú formuláciu Raschovho modelu a je prekvapivo podobná tej mojej (a porovnateľne jednoduchá). Napríklad, rovnako ako môj model, uvažuje parametre reprezentujúce ako kvalitu žiakov, tak aj kvalitu otázok a navyše modeluje pravdepodobnosť správneho zodpovedania otázky žiakom ako funkciu rozdielu parametra otázky a parametra žiaka. Rozdiel je len v tom, že moja funkcia vyjadrujúca výslednú pravdepodobnosť je po častiach lineárna, definovaná na množine (0,1)x(0,1) a Raschova je logistická, definovaná na RxR (obe sú navyše rovnakým spôsobom monotónne v parametroch). Táto podobnosť má za následok aj podobné simulačné výsledky, najmä to, že výsledky majú často veľmi negaussovské rozdelenie, ako sa môžete presvedčiť. Snáď Raschovmu vzorčeku už nebudete vyčítať, že nie je ničím podložený :). A a pritom komplexnejšie modely by umožňovali ešte lepší fit s napozorovanými dátami. Ja verím, že máte veľa skúseností s testovaním žiakov, ale zasa ja mám veľa skúseností s dátami, modelmi, simuláciami a pravdepodobnostnými rozdeleniami a práve na tých sa zakladalo Vaše zdôvodnenie obviňovania tisícov ľudí z podvádzania. Ste určite veľmi skúsený odborník, ale pri podobných argumentáciách, najmä založených na matematike, treba byť podľa mňa trochu opatrnejší.
Juro: Asi by sme sa vo väčšine vecí zhodli. Súhlasím, že nie vždy je najlepšie založiť úvahy na modeli a že vždy sa musí model prispôsobovať datam, nie naopak. Ale pán Burjan vo svojej argumentácii použil práve model presným gaussovským rozdelením a to v situácii, kde je tento modelový predpoklad (gaussovského rozdelenia) vyložene nevhodný. Inak jeho intuícii a skúsenostiam verím aj ja.
Peter Burjan: Ako vidíte na tom Raschovom modeli, aj keď som generoval schopnosti žiakov z normálneho rozdelenia, celkové výsledky nemajú normálne rozdelenie (a nemali by presne normálne rozdelenie ani v mojom pôvodnom modeli), čiže Vaše tvrdenie je jednoducho chybné. Okrem toho aj ja sa môžem oprieť o empirické údaje, pretože som roky robil testy na skupinách veľkosti okolo 120 študentov a rozdelenie výsledkov nebolo ani zďaleka normálne; niekedy bolo dokonca zjavne multimodálne, pretože obsahovalo celé skupiny podobne dobrých (alebo zlých) študentov. Tvrdenie, že ak stredné hodnoty úrovne škôl majú normálne rozdelenie a výsledky žiakov v rámci každej školy majú normálne rozdelenie (so strednou hodnotou danou úrovňou príslušnej školy), tak sumárne výsledky budú mať normálne rozdelenie, je tiež omyl, hoci laikovi by sa to mohlo tak javiť. Výsledné rozdelenie bude mať nižšiu špicatosť. Ja nikde neopakujem chybu, že systém sa bude podobať výsledku môjho nie úplne reálneho modelu (žiadny model nie je úplne reálny); ja ukazujem jeden model, ktorý bude zjavne dávať podobné (negaussovské) výsledky ako celá trieda príbuzných modelov (napríklad Raschov model), medzi ktorými sa *môže* vyskytovať správny model (nikto nikde nedal argument, že sa nemôže). Už len to, že *môže existovať* reálny model, ktorý dáva negaussovské výsledky, spochybňuje argumentáciu pána Burjana založenú na predpoklade presnej normality. To je pomerne elementárna logika, ktorej vy zjavne nerozumiete. Tiež by sme sa ešte mohli porozprávať o tom Vašom super modeli, ktorým ste ma predtým poúčali, a na ktorý ste po mojej odpovedi nejako pozabudli.
Je inak pre mňa dosť prekvapivé (až komické) s akou istotou sa vyjadrujete a dokonca poučujete o veciach, v ktorých nemáte žiadnu kvalifikáciu, často dokonca ani šajnu. A ešte ma aj osobne urážate. Pripúšťam, že aj moje úvahy, komentáre a podobne môžu byť niekedy chybné, alebo zjednodušené (nakoniec, toto je nezáväzný blog, nie vedecký článok) a som rád, keď ich niekto konštruktívne skritizuje. Ale vy jednoducho len povýšenecky trepete z dve na tri.
Posledná časť predchádzúceho príspevku patrí samozrejme pre Petra Bozeka, nie pána Vladimíra Burjana.
Rado, som rad ze si zacal pouzivat normalne rozdelenie, poznacil som si to do zosita ako dobry skutok na tento den. Len dalej na sebe pracuj. Len neviem preco tomu hovoris Raschov model, pri vsetkoej skromnosti je to bozekov model :-)
Len dve poznamky: Ano, zmenou funkcie V sa da tvar funkcie ovplyvnit, ale poziadavka monotonnosti znacne zuzuje moznosti ako - stale to bude modifikovana Gaussova krivka. Mozes Gaussovu krivku rozsirit alebo zuzit (stacilo zvolit vhodnu standardnu odchylku) ale nemozes dostat dve vrcholy, napriklad (aspon myslim) takze pochybujem ze dostanes nieco podobne udajom.
Za druhe, uz sa nebavime o tom ze jednoduchy model vedie k tvaru podobnemu udajom, bavime sa o tom ze aby sa dala ziskat krivka aspon trochu podobna datam, je treba zvolit velmi specificke rozdelenie zlozitosti otazok. A v tomto okamziku nastupuje Occamova britva, ze.
Pan Bozek, ak si clovek precita Vase prispevky v tejto diskusii, zisti dve (smutne) veci:
- uporne a trapne sa snazite vydrazdit pana Harmana,
- kedykolvek Vam dokaze, ze veci nerozumiete (a stalo sa to uz viackrat), prejdete to mlcanim a svoje bludy opakujete podla znameho Goebbelsovho principu.
Vychadza mi z toho, ze s Vami nieco nie je v poriadku, ale dufam, ze sa z toho casom dostanete.
Ad Peter Bozek:
"Rado, som rad ze si zacal pouzivat normalne rozdelenie, poznacil som si to do zosita ako dobry skutok na tento den."
V simulácii Raschovho modelu som použil normálne rozdelenie na generovanie parametra kvality žiakov z toho dôvodu, aby neboli pochybnosti, že aj normálne rozdelenie kvalít žiakov môže viesť k histogramu výsledkov, ktorý má od Gaussovej krivky veľmi ďaleko.
Inak, normálne rozdelenie niekedy veľmi presne opisuje dáta, inokedy však vôbec nie, takže to, či použiť normálne rozdelenie, treba posudzovať prípad od prípadu. Ukazuje sa, že reálne dáta sú len málokedy presne normálne rozdelené a práve pri väčších rozsahoch výberu je odchýlka od normality ľahšie overiteľná (takzvanými testami normality). Na spracovanie dát, ktoré nie sú normálne, existujú celé štatistické oblasti (napríklad robustná štatistika a neparametrická štatistika). Okrem toho v niektorých situáciách je aj pri ideálnych (čisto teoretických) podmienkach rozdelenie dát úplne odlišné od normálneho, napríklad pri modelovaní extremálnych hodnôt.
"Len dalej na sebe pracuj. Len neviem preco tomu hovoris Raschov model, pri vsetkoej skromnosti je to bozekov model :-)"
To čo som naprogramoval som nazval Raschov model, pretože ten model sa tak štandardne nazýva, pozrite napríklad tu. Raschovmu modelu totiž, celkom prirodzene, verí pán Burjan viac ako môjmu modelu (oba modely inak majú veľa spoločných čŕt). To čo ste navrhli Vy som neprogramoval.
"Len dve poznamky: Ano, zmenou funkcie V sa da tvar funkcie ovplyvnit, ale poziadavka monotonnosti znacne zuzuje moznosti ako - stale to bude modifikovana Gaussova krivka. Mozes Gaussovu krivku rozsirit alebo zuzit (stacilo zvolit vhodnu standardnu odchylku) ale nemozes dostat dve vrcholy, napriklad (aspon myslim) takze pochybujem ze dostanes nieco podobne udajom."
Pokiaľ som ten Váš model pochopil správne (neposkytli ste totiž presnú matematickú formuláciu a k mojej formulácii Vášho modelu ste nevyjadrili námietky), tak zmena funkcie V v rámci triedy monotónnych funkcií neznižuje možnosti výsledného tvaru rozdelenia.
Uvediem konkrétny príklad (nebudem dokazovať všeobecné tvrdenie). Nech F je distribučná funkcia zodpovedajúca zmesi dvoch regulárnych normálnych rozdelení, takej, že hustota prislúchajúca k F má "dva vrcholy", čiže dve lokálne maximá. Funkcia F je hladká a monotónne rastúca; nech F^{-1} je jej inverzia (nazývaná tiež kvantilová funkcia). Položme V(.)=F^{-1}(N(.)), kde N je Vami uvažovaná distribučná funkcia normálneho rozdelenia. Takto definovaná funkcia V je hladká, monotónne rastúca a zároveň očividne V^{-1}(.)=N^{-1}(F(.)). Potom však platí N(V^{-1}(n))=N(N^{-1}(F(.)))=F(.), čiže výsledné rozdelenie má distribučnú funkciu F, i.e., "dva vrcholy". Tieto úvahy inak veľmi úzko súvisia s takzvanou metódou inverznej transformácie.
"Za druhe, uz sa nebavime o tom ze jednoduchy model vedie k tvaru podobnemu udajom, bavime sa o tom ze aby sa dala ziskat krivka aspon trochu podobna datam, je treba zvolit velmi specificke rozdelenie zlozitosti otazok. A v tomto okamziku nastupuje Occamova britva, ze."
V tom Raschovom modeli som práveže pre jednoduchosť zvolil úplne rovnakú náročnosť otázok, ako sa môžete sami presvedčiť z programového kódu. Napriek tomu sú celkové bodové výsledky veľmi odlišné od normálneho rozdelenia. Okrem toho však obtiažnosti otázok kľudne mohli byť (a v skutočnosti zrejme aj boli) rôznorodé, čo by mohlo viesť k ešte komplikovanejším tvarom výsledného histogramu.
Pán Peter Bozek, ospravedlňujem sa, ale už naozaj nemám čas Vám všetko vysvetľovať; musím sa totiž primárne venovať mojim vlastným študentom a vedeckému výskumu.
Prajem Vám pekný deň,
RH
PS: Nikdy nevylučujem, že sa mýlim, takže samozrejme ak by sa ozval so svojimi argumentami niekto, kto sa do problematiky rozumie (ako napríklad pán Burjan), tak reagovať budem.
Len pre zaujímavosť prikladám niektoré dáta zo svojej stránky: www.otestujsa.sk/data/otestujsaTesty.zip
Sú tam aj staré testy Testovanie 9 (ešte po starom Monitor) a staré testy na vodičák.
Sú filtrované tak, že som vyhodil opakovaný test toho istého užívateľa (testy sú anonymné a je to podľa cookies, takže nie je to na 100 %).
Stránka beží už od roku 2008.
Tak trochu na tému známok a ich falšovania.
Zverejnenie komentára