Tri trojuholníky

Problémy optimálneho navrhovania experimentov, čo je moja hlavná oblasť výskumu, sú prekvapivo pestré, pretože zasahujú do takmer všetkých matematických disciplín: od štatistiky a pravdepodobnosti, cez kombinatoriku, teóriu grafov, analýzu, lineárnu algebru, teóriu matíc, až po numerickú matematiku. Dnes sa mi pri písaní článku z tejto oblasti dokonca vyskytlo jednoduché tvrdenie z klasickej rovinnej geometrie; formulujme si ho ako úlohu.

Majme päť priamok p₁, p₂, q₁, q₂, q₃, ako je znázornené na obrázku, pričom priamky q₁, q₂, q₃ sú rovnobežné. Označme ako A_ij prienik priamok p_i a q_j. Dokážte, že súčet obsahov trojuholníkov A₁₁A₁₂A₂₃ a A₁₂A₁₃A₂₁ je rovný obsahu trojuholníka A₁₁A₁₃A₂₂.

Koľko matematikov, toľko dôkazov

Nasledovná jednoduchá, ale celkom pekná dôkazová úloha sa nám objavila pri písaní článku o optimálnom navrhovaní experimentov pre náhodné procesy. Spomenuli sme ju viacerým kolegom a každý prišiel po nejakom čase so svojim vlastným dôkazom. Som zvedavý, koľko rôznych dôkazov sa podarí nájsť Vám.

Ukážte, že ak hladká funkcia f:R→R spĺňa rovnicu

pre všetky reálne čísla x a všetky kladné reálne čísla δ, potom je f kvadratická funkcia.

Kvadratickou funkciu rozumieme aj lineárnu a konštantnú funkciu (s niektorými koeficientmi nulovými). Ako obvykle, symbol f ' označuje deriváciu funkcie f.

Konvexné smery

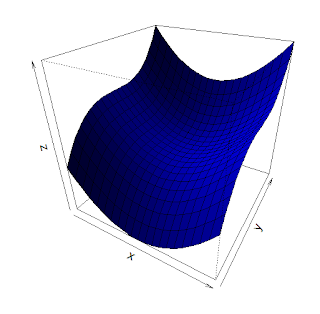
Nech f je reálna funkcia definovaná na množine všetkých dvojíc reálnych čísiel. Smerom nazveme každý vektor (u,v) jednotkovej dĺžky.  Budeme hovoriť, že funkcia f je konvexná v smere (u,v), ak pre každý bod (a,b) je konvexnou funkcia priradzujúca číslu α číslo f(a+αu,b+αv). Je zrejmé, že ak je funkcia f konvexná vo všetkých smeroch, tak je sama konvexná. Konvexnosť v jednom smere však samozrejme nestačí; napríklad nekonvexná funkcia f(x,y)=x²+y³ je konvexná v smere (1,0):

Stačí na zabezpečenie konvexnosti funkcie f konvexnosť v dvoch rôznych smeroch? V troch? ...

Aké je maximálne prirodzené číslo n, pre ktoré existuje nekonvexná reálna funkcia f  dvoch reálnych premenných, ktorá je konvexná v n rôznych smeroch (u₁,v₁), ... ,(u_n,v_n)?

Hlavolam z výstavy

Dnes som sa v rámci nedeľného oddychu vybral s manželkou a dcérkou do Slovenského národného múzea na výstavu "Matematika pre potešenie". Aj keď na prvý pohľad pôsobí táto výstavka pomerne chudobne, dá na nej celkom dobre zabaviť, čo platí dvojnásobne, ak máte so sebou dieťa :). Väčšina exponátov je založená na dobre známych princípoch, napríklad Galtonova skrinka, Buffonova ihla, Kreslenie grafu jedným ťahom, Möbiusov list, Tangram a podobne. Mňa najviac zaujalo vedro s mydlovou vodou, do ktorého bolo možné ponárať drôtené modely telies (napríklad kocka, pravidelný simplex, štvorboký ihlan) a sledovať tvar vzniknutých membrán, podobne ako v jednom našom staršom príspevku.

Výstavka obsahuje aj niekoľko hlavolamov, z ktorých sa mi jeden nepodarilo vyriešiť, hoci som nad ním strávil možno aj štvrť hodiny. (Trochu ma to rozladilo, pretože riešenie je určite veľmi jednoduché. :) Vy však možno budete úspešnejší ...

Poskladajte štvorec rozmerov 6x6 z ôsmich kúskov znázornených na nasledovnom obrázku.

How long will it take Marie to saw a board into 3 pieces?

K napísaniu tejto rekreačnej úlohy ma inšpiroval príspevok Math teacher fail na blogu TYWKIWDBI (credits: Lenka Filová). Za normálnych okolností, t.j. ak pod slovom "board" rozumieme obdĺžnikovú dosku, je odpoveď učiteľa nesprávna. Ale... :)

Márii trvá 1 minútu, kým rozpíli drevený útvar konštantnej hrúbky na 2 rovnaké časti. Ako dlho bude trvať Márii, kým rozpíli tento útvar na 3 rovnaké časti? Aké sú všetky možné "správne" odpovede v závislosti od tvaru tohto útvaru?

Uvažujeme len také útvary, ktoré je možné rozpíliť na dve aj na tri rovnaké časti a tiež predpokladáme, že Mária píli daný útvar najkratším možným rezom (alebo najkratším možným súčtom dĺžok rezov), po ktorom sa rozpadne na dve, resp. tri rovnaké časti. Na to, aby sme dve časti považovali za "rovnaké", nestačí, aby boli "zrkadlovo rovnaké" (povedzme, že strany dosky sú ofarbené rôznymi farbami, čo umožní rozlíšiť zrkadlovú podobnosť od skutočnej zhodnosti).

Kedy sa obsah rovná dĺžke

Nasledovná úloha ma napadla keď sme dnes písali zovšeobecnenie nášho článku o generovaní náhodných bodov na mnohorozmerných sférach. 

Množinu M v rovine nazývame hviezdicovo konvexnou, ak v nej existuje "centrálny" bod O, z ktorého je "vidieť" všetky body množiny M, čiže ak pre každý bod A množiny M platí, že úsečka OA je celá v množine M. Pre jednoduchosť budeme uvažovať len tie hviezdicovo konvexné množiny, ktoré sú ohraničené, a pre ktoré je centrálnym bodom bod O=(0,0).

Výsekom hviezdicovej množiny M určeným bodmi X,Y ležiacimi na hranici M nazveme útvar ohraničený úsečkami OX, OY a krivkou, ktorá tvorí hranicu množiny M medzi bodmi X a Y. (Na tomto mieste a aj ďalej predpokladáme, že sa pohybujeme od bodu X k bodu Y po hranici množiny M v "smere hodinových ručičiek"). Na ilustračnom obrázku je množina M modrá a výsek určený bodmi X,Y je červený:

Všimnime si, že kruh v rovine so stredom v O a polomerom 2 má nasledovnú vlastnosť: obsah výseku určeného hraničnými bodmi X,Y je presne rovný vzdialenosti bodov X a Y po hraničnej kružnici.

Otázka znie: Existujú aj iné hviezdicovo konvexné množiny M s vlastnosťou, že obsah výseku množiny M určeného hraničnými bodmi X a Y je rovný vzdialenosti bodov X,Y po hranici množiny M?

Poznámka: Nedefinovali sme síce presne, čo je to hranica množiny M a čo je to vzdialenosť hraničných bodov X,Y "po hranici", ale tieto pojmy by mali byť intuitívne dostatočne jasné na pochopenia jadra zadania, bez rozptyľovania sa exaktnými, no komplikovanými formálnymi definíciami.


16.8.: Riešenie úlohy nám do komentárov napísal Ivan. Stručne, množín s danou vlastnosťou je nekonečne veľa, napríklad ak dotyčnice ku hranici, všade tam, kde jednoznačné dotyčnice existujú, sú priamky vo vzdialenosti 2 od bodu O. Taká je aj nasledovná "hviezda" :)

Pochopiteľne, existuje mnoho ďalších otázok, ktoré by sme sa mohli spýtať, napríklad: 1) Je každá množina s uvedenou vlastnosťou prienikom a zjednotením systému polrovín určených priamkami vzdialenými o 2 od bodu O? 2) Aké množiny "s oblými hranicami", t.j. nie polygóny, majú túto vlastnosť? 3) Aké je zovšeobecnenie tejto úlohy do viacrozmerného priestoru?

Nočná pyramída o pravdepodobnosti a logike

Zajtra (v sobotu 29.5.) o 22:30 budem spolu s profesorom Anatolijom Dvurečenskim hosťom relácie "Nočná pyramída" Slovenského rozhlasu. Takže ak máte čas, budem veľmi rád, keď si nás vypočujete.

Pred pár hodinami som dostal scenár a je skutočne zaujímavý. Základné témy sú "teória pravdepodobnosti", "vzťah medzi matematikou a logikou", "možné svety" a "náhoda a nutnosť". Trochu je problém v tom, že väčšina (predbežných) otázok má buď komplikované, alebo dosiaľ neznáme odpovede, prípadne na ne odpoveď asi vôbec ani neexistuje... Ale o to väčšia zábava bude na ne odpovedať, takže sa na to veľmi teším :)

30.5.: Kompletný záznam relácie vo formáte mp3 si môžete stiahnuť na tejto adrese. Veľmi rád Vám odpoviem na akékoľvek (ďalšie) otázky k téme.

Éter v štvorrozmernom priestore

Minulý týždeň som konečne odovzdal habilitačnú prácu, odoslal som náš najnovší článok a navyše sa skončilo vyučovanie, takže sa opäť s radosťou vraciam k môjmu blogu :) Mali sme tu už viaceré úlohy z geometrie v rovine aj v priestore. Čo by ste ale povedali na úlohu z geometrie v hyperpriestore?

Predstavme si dvojrozmerných obyvateľov povrchu sférickej planéty, ktorá rotuje okolo svojej osi v nehybnom éteri. Títo obyvatelia síce nevedia vnímať tretí rozmer, ale pohyb povrchu svojej planéty voči éteru odmerať vedia. To znamená, že na istej do seba uzavretej priamke (z nášho pohľadu na rovníku planéty) pozorujú najvyššiu rýchlosť pohybu éteru a v dvoch špeciálnych bodoch (z nášho pohľadu na póloch) pozorujú nulovú rýchlosť pohybu éteru.

Moja otázka znie: Ak by náš trojrozmerný vesmír bol povrchom štvorrozmernej gule rotujúcej v nehybnom štvorrozmernom éteri a vedeli by sme odmerať relatívnu rýchlosť tohto éteru voči nám, ako by sme vnímali oblasti najrýchlejšieho pohybu éteru (čiže akýsi švorrozmerný rovník) a ako by sme vnímali oblasti nulovej rýchlosti pohybu éteru (čiže štvorrozmerné póly)?